Topologiska identiteter
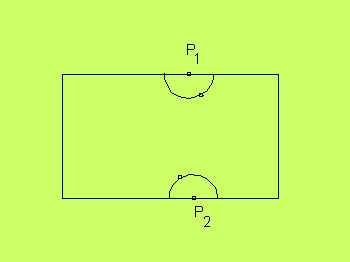
Givet en ett topologiskt rum, S, med en rand. Vi kan säga att en
punkt P1 på
randen är identifierad med en annan punkt P2 på randen
skrivet P1 ~ P2. Detta representerar
någon slags slutenhet, där vi, då vi kommer från S till punkten
P1 kan fortsätta från P2 till en annan del
av S. På detta sätt kan vi t.ex. låta en fyrkantig karta
representera en cylinder.
Denna idé kan vi formalisera genom att skapa en
topologi med kluvna klot. Vi utgår
från den "vanliga topologin", som baseras på klot som baseras p�
metriker. Vi modifierar den vanliga metriken d till en metrik
d' på följande
sätt:
d'(x,y)=min(d(x,y), min(d(x,P1)+d(P2,y)))
där det andra minimat tages över alla
P1 och P2 sådana att
P1 ~ P2.

Om vi alltså kan hitta en genväg från x till y via ett par av
identifierade punkter, så låter vi den bestämma avståndet.
De klot, som genereras av den här modifierade metriken,
blir kluvna klot, som har en del i anslutning till P1
och en del i anslutning till P2
På samma sätt kan vi göra med en mängd som består av flera
delar (komponenter). Vi kan identifiera en punkt på randen
av en komponent med randen av annan punkt på en annan komponent
Möbiuskartor
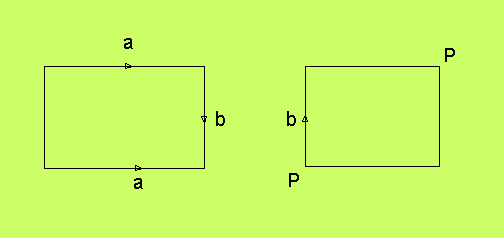
En möbiuskarta består av rektangulära kartor där kanter som
har identifierade sidor är markerade. Identifierade punkter
behöver inte markeras punkt för punkt, utan man markerar bara
en riktning på vardera kanten, som talar om i vilken ordning
de identifierade punkterna dyker upp. Dessutom måste man ange
en identiferande symbol vid de båda kanterna. Därutöver kan
hörnpunkter vara identiferade, vilket också markeras med
symboler.
Varje rektangulär delkarta representerar en yta som genom
sträckning, skjuvning, böjning m.m. kan deformeras till
en rektangel.Möbiuskartans uppgift är att beskriva
slutenhetsegenskaper hos ytan.
I andra dimensioner än 2 kan en Möbiuskarta bestå av linjer
eller parallellepipeder (dim 3) eller hyperparallellepipeder
(dim > 3). En cirkel representeras t.ex. av en möbiuskarta, som
är en ändlig rät linje, där ändpunkterna är identifierade.
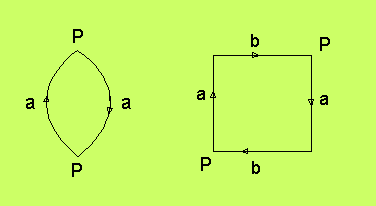
Exempel på Möbiuskartor
Cirkeln Cirkeln beskrivs alltså av följande Möbiuskarta:

Från en punkt nära P till höger kan man komma vidare vid P
till vänster.
Cylinder Cylindern beskrivs av följande Möbiuskarta:
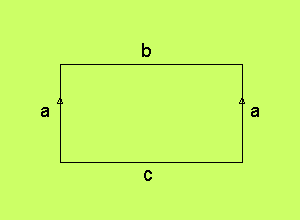
Sidorna b och b i kartan är inte identifierade med några andra
sidor och representerar därför cylinderns rand. Vi kan
rulla ihop figuren till ett rör och klistra fast a mot a. Men
vi kan också tånja ut figuren i ena kanten och tillverka en
rund skiva med ett hål. Dessa två figurer är topologiskt identiska.
Man kan deformera den egna figuren till den andra, utan att
punkter som ligger nära varandra kommer långt ifrån varandra.

Möbiusbandet. I nästa figur har vi vänt riktningen på
en av de identiferade pilarna:
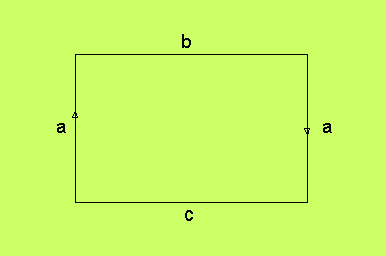
Den tredimensionella figuren blir ett vridet band, kallat
Möbiusbandet.

Den har en rand, som består av sidorna b och c
men de sidorna hänger ihop, för ena ändpunkten på b är identisk
med den andra ändpunkten på c eftersom de båda är "bakänden" på
sidan a, och samma sak gäller också för "framänden" på a.
Ett Möbiusband har därför bara en kant, som löper två varv runt
figuren. I teorin för
dynamiska system svarar Möbiusbandet
därför mot ett fenomen som kallas periodfördubbling.
Möbiusbandet kan plattas ut liksom cylindern, men det kan inte
bli en helt plan figur; den måste bubbla upp i en tredje
dimension vid vridningen.
Rösslers band, Man kan kombinera en cylinder och ett
Möbiusband till en figur som är både vriden och icke vriden,
och som kallas Rösslers band. Nedan syns både Möbiuskartan och
en tredimensionell realisering av figuren. En hjälppil i båda
figurerna visar hur man avlägsnar sig från linjen a.
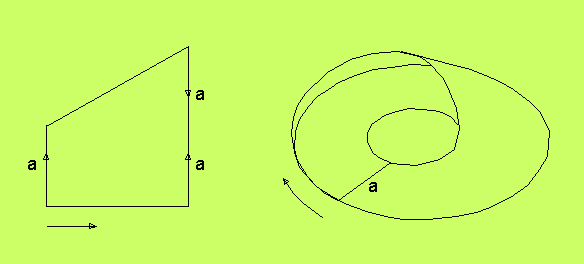
Figuren har alltså kluvna klot (eg. cirkelskivor),som består
av tre delar. Den är inte helt lätthanterlig teoretiskt som
mångfald, men den är viktig som
tillståndsrum för ett dynamiskt
system, som kan uppvisa kaos.
Torusen. Om man identifierar de båda delarna av randen
till en cylinder, så svarar det mot att man måste rulla ihop
cylinderröret och klistra ihop rörändarna. Man får en torus.
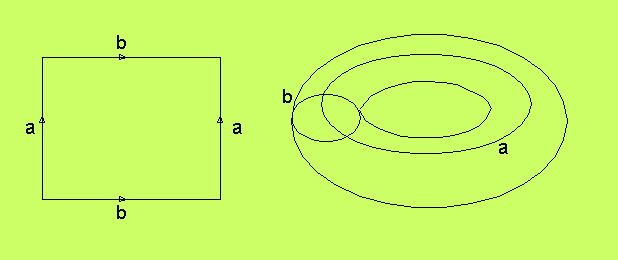
Torusen år en sluten figur, dvs den saknar rand. Den
tredimensionella representationen är en smula osymmetrisk vad
gäller de båda identifierade sidorna a och b, medan Möbiuskartan
är helt symmetrisk. Därför gör sig torusen egentligen bättre
i en fyrdimensionell värld. Torusen kan konstrueras som den
Cartesiska produkten mellan två cirklar, och betecknas därför
med S1 × S1, där S1 betecknar
cirkeln (den endimensionella sfären.). I teorin för dynamiska
system representerar torusen ett system med två oberoende
oscillatorer (svarande mot var sin cirkel). Man kan gå vidare
till S1 × S1 × S1.
Kleins flaska. Om man vänder på identifieringen på
cylinderröret, så får man svårt att rulla ihop röret så att
rörändarna är orienterade på rätt sätt. En lösning är att sticka
in den ena röränden i röret. Resultatet kallas Kleins flaska:
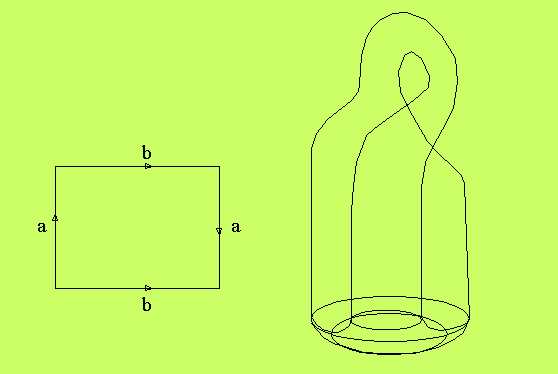
Att ytan skär sig själv, där halsen går in i flaskkroppen, är
ett fenomen, som inte har någon motsvarighet i Möbiuskartan.
Det är en topologisk defekt, som innebär att en Kleinsk flaska
egentligen inte kan realiseras i tre dimensioner.
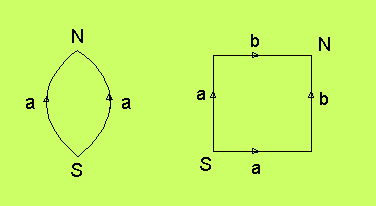
Sfären. Möbiuskartan för en sfär ser ut så här; till
höger i en kantigare variant, där vi har delat upp sträckan
a i två delsträckor. Punkterna N och S (som inte är identifierade)
kan vara nord- och sydpolen, och sträckan a kan vara en meridian
(longitud) t.ex. 180-graders-meridianen.
Den vridna sfären. Om man vänder på en av pilarna i
kartan för en sfär, så får man en figur, som inte lätt går
att återge i tre dimensioner, kallad den vridna sfären.
Observera att det är en unipolär figur, alltså att nord- och
sydpolen sammanfaller. Den vridna sfåren, även kallad
det projektiva planet representerar mängden av oändligt
långa räta linjer som passerar genom origo. Varje sådan linje
skär enhetssfären på två ställen. Om man svänger runt en linje
180 grader, får man samma linje. Därför kan man representera
varje linje med sin skärningspunkt på den nedre halvsfären. Men
linjer i horisontalplanet skär ändå halvsfären i tvä punkter.
De båda skärningspunkterna representerar samma linje och år då
identifierade. Därmed har vi en halvsfär med en kant med
identifierade punkter. Efter tillplattning får vi den plana
Möbiuskartan ovan.
SO(3,R). Lie-gruppen
SO(3,R) representerar alla
vridningstillstånd hos en stel kropp. Euler har visat att
varje vridningstillstånd kan nås från ett referenstillstånd
med hjälp av en vridning kring en axel.
Vridningsaxeln kan representeras som en linje från origo, och
vridningens storlek kan representeras som en längd hos linjen.
Men vridningar med en vinkel α är identiska med vridningar
med vinklar α+n·2π. Därför behöver vi bara
representera ett vinkelintervall som är 2π stort. Det är
naturligt att då lägga det mellan -π och π. Men
ändpunkterna på en sådan linje representerar samma
vridningstillstånd,
för en vridning framåt med π radianer ger samma
resultat som en vridning bakåt med π radianer. En Möbiuskarta
för SO(3,R) är därför en sfär med radien π och
med varje punkt identifierad med sin antipod.

Orienterbara och icke orienterbara mångfalder
Somliga av de mångfalder, som vi har presenterat ovan
har varit "vridna". En mera officiell beteckning på de
icke-vridna mångfalderna är, att de är orienterbara.
I två
dimensioner är det relativt lätt att avgöra vilka mångfalder
som är orienterbara. Om man rör sig runt kanten på
Möbiuskartan, och stöter på två identifierade sidor, så
kan de peka mot varandra. Då säger man att man har ett
toroidpar. Om de pekar med varandra (alltså båda med eller
båda mot färdriktningen runt kanten) så säger man att man
har ett vridet par. Det vridna paret känneteckar en vriden,
alltså icke-orienterbar, mångfald. Man kan visa att existensen
av ett vridet par är en "dominant" egenskap, dvs om det
finns ett vridet par, så kan man klippa sönder och klistra
ihop Möbiuskartan, tills alla par är vridna. Figuren visar
ett exempel, där utgångsläget är Möbiuskartan för Kleins flaska:
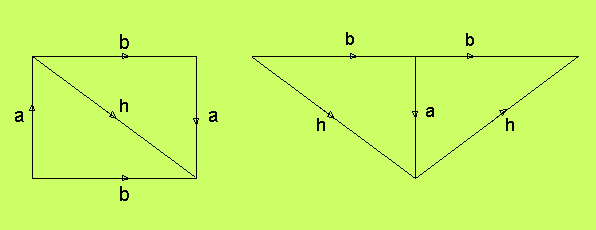
I den vänstra figuren har vi ritat in en diagonal,h, längs
vilken vi klipper sönder figuren. Dårefter vrider vi den ena
triangeln, så att vi kan klistra ihop a mot a med rätt
identifieringsordning. Nu har vi bara vridna par.
Därmed kommer alla slutna ytor att falla i en av två kategorier,
orienterbara och icke orienterbara.
I högre dimensioner än 2 får man använda andra kriterier. Det
allmänna kriteriet har att göra med de koordinatbytesfunktioner
som dyker upp då man flyttar sig från en karta till en annan
i en atlas. Koordinatbytesfunktionen
ges som b=xk ○
(xj)-1.
Koordinatbytesfunktionen kan lineariseras i en punkt, vilket
ger en matris (Jacobianen) med element:
Jkj = ∂bk/∂xj
Om Jacobianen har en negativ determinant, så betyder det i
någon mening att koordinatbytesfunktionen byter orientering.
Frågan är nu om man kan röra sig runt i varje sluten slinga
runt de olika kartorna i en atlas, och komma tillbaka med samma
orientering som man startade i. Man kan alltid byta koordinat
funktioner, utan att strukturen hos atlasen förändras. Ett
alternativt kriterium är då detta: Kan man byta koordinatfunktioner,
så att alla koordinatbytes-Jacobianer får positiv determinant? I
så fall är mångfalden orienterad.
Rösslers band var både orienterad och icke-orienterad på en gång,
och faller därmed utanför ramen för satsen att varje mångfald,
är antingen eller. Men Rösslers band uppfyller inte kriterierna
för en mångfald.
Simpliciala komplex
Ett simplex är ett geometrisk objekt som
representeras av en Möbiuskarta med en rektangel (linje
parallellepiped etc), där inga kanter och inga
hörnpunkter är identiferade.
Ett simplicialt komplex C är ett geometriskt objekt
som representeras av en uppsättning av Möbiuskartor för
simplex, där somliga kanter är identifierade med somliga
andra kanter.Vi inför beteckningen S för mängden
av punkter som tillhör någon Möbiuskarta i denna
uppsättning av Möbiuskartor. Punkterna har sina
identifieringsegenskaper med sig i S, och punkter,
som är identifierade skall betraktas som identiska.
Varje delmängd
Si av S, genererar automatiskt ett (enklare)
simplicialt komplex, som kallas Ci. Vi har alltså
en avbildning F från varje Si till motsvarande
Ci. F motsvarar proceduren: tag alla Möbiuskartorna
som bygger upp Si och sätt ihop dem genom att
klistra ihop identifierade punkter.
När representationen av C med S är given,
är F inverterbar, alltså en isomorfism
Inför nu en operation Δ, som ges av
M Δ N = mängden av alla element, som tillhör M eller N men
inte båda
F avbildar denna mängdoperation på en operation för simpliciala
komplex, som kallas +.
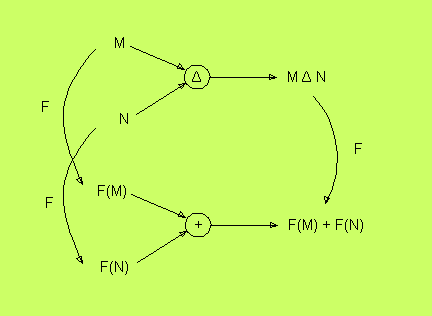
F avbildar ∅, den
tomma mängden av Möbiuskartor på det tomma komplexet, som
kallas 0.
Mängden av komplex, som genereras av F från en mängd Möbiuskartor,
tillsammans med +, bildar en grupp. Enhetselementet är 0.
Varje element är sin egen invers.
Randen till ett simplicialt komplex
Randen till ett simplicialt komplex C betecknas med
∂C.
Randen till ett simplex definieras på följande sätt:
I dimension 0 är randen till en punkt den tomma mängden
∅.
I dimension 1 är randen till en linje dess båda ändpunkter.
I dimension 2 är randen till en rektangel dess kanter.
I dimension 3 är randen till en parallellepiped dess kantytor
Randen till ett simplicialt komplex definieras nu av följande
regel:
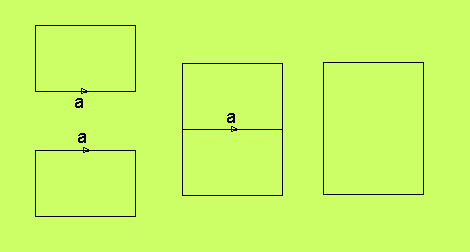
∂(A+B) = ∂A + ∂B
Låt A och B svara mot var sin Möbiuskarta med en av sidorna
identifierade. ∂A svarar då mot de fyra kanterna av
A's Möbiuskarta. ∂B svarar mot de fyra kanterna av
B's Möbiuskarta. Men den identifierade sidan uppträder
då i båda, och försvinner då genom operationen Δ. I komplexet
∂(A+B) försvinner den då genom operationen +.
Slutna komplex och ränder
Ett simplicialt komplex C kallas slutet, om
∂C = 0
Ett simplicialt komplex C kallas en rand om det
är en rand till något, dvs om det existerar ett
komplex A så att
C = ∂A
En rand år alltid sluten, vilket kan skrivas
∂∂A = 0 för alla A
men ett slutet komplex år inte
en alltid en rand. Typexemplet är att det slutna komplexet
omsluter ett hål. Randen till det inneslutna området är då
det slutna komplexet + randen till hålet. Det slutna
komplexet ensamt är alltså inte en rand.
De hår begreppen har en motsvarighet i teorin för
differentiella former.
En differentiell form ω kallas sluten om
dω = 0
En differentiell form ω kallas exakt, om den är
differentialen av någon differentiell form β, dvs om
ω= dβ
En exakt form är sluten, vilket skrivs som
ddβ = 0
Men det år en öppen fråga om en sluten differentiell form
år exakt. De båda frågorna om en sluten differentiell form
är exakt och om ett slutet simplicialt komplex är en rand,
år relaterade via Stokes' sats.
Homologi
Med hjälp av begreppet rand och operationen + kan man bilda
en ekvivalensrelation, kallad homologi, eller att vara homolog
med. Två simpliciala komplex C och D är homologa, skrivet
C ~ D
om
C + D är en rand
En rand R är homolog med det tomma komplexet för
R + 0 = R som är en rand
Därmed är enligt transitiviteten hos
~
alla rånder homologa med varandra, och bildar en
ekvivalensklass
med 0 som representatant. Om en komplex C omsluter
ett hål med randen H, men inget annat hål, så ä C homologt med
H, eftersom
C + H är en rand
Därmed är alla komplex som bara omsluter det hålet homologa,
och bildar en ekvivalensklass med H som en representant. H är
nåmligen homolog med sig sjålv,
H~H, för
H+H=0 som är en rand. På det här sättet kommer mängden
av ekvivalensklasser med avseende på
~ att karakterisera
de topologiska egenskaperna hos en mångfald.
















