Dynamiska System
Ett dynamiskt system är ett deterministiskt system,
alltså ett system, vars framtid är förutbestämt.
Till ett dynamiskt system hör en mängd, kallas
tillståndsrummet. Tillståndsrummet är vanligtvis
ett topologiskt rum och dess
element kallas då punkter, och de kallas också för
tillstånd. I rummet skall finnas kurvor γ, kallade
orbits, med följande egenskap:
Varje punkt p i tillståndsrummet skall
passeras av en unik orbit, kallad γp, dvs för något
T(p) skall värdet γpT(p) av funktionen
γp vara = p.
Denna kurva bestämmer systemets framtida tillstånd på
följande sätt:
Om tillståndet är p vid t, så är det
p1 = γp
t1-t+T(p)
vid tiden t1
Om vi först väljer p och sedan kallar γp för
γ och sedan indexerar om kurvan, så att den passerar p
vid t=0, så får vi följande förenklade utsaga:
Om tillståndet är p vid t, så är det
p1 = γt1-t
vid t1
Vi föreställer oss gärna att variabeln t, som är avsatt längs
varje orbit, representerar tiden.
Om tillståndsrummet är en mångfald M, så är varje orbit, γ,
en funktion från R till M. Tillståndet p kan nu representeras
med de n koordinaterna xi(p) för p. En orbit kan
representeras med en funktion från R till Rn.
Det följer av definitionen, att två olika orbits inte kan
utgå från samma punkt. Orbits kan då inte korsa varandra,
och inte heller dela sig. Däremot kan två olika orbits löpa
samman. I vissa sammanhang kräver man att ett dynamiskt system,
för att få kallas så, också skall vara ett dynamiskt system i
bakåtgående tid. I så fall kan orbits inte heller löpa samman.
Dynamiska system som grupp
Om vi från p har kommit till p1, så kan vi fortsätta
därifrån till ett framdida tillstånd p2 med det
fullständigare uttrycket ovan:
p2 = γp1
t2-t1-T(p1)
Denna centrala egenskap kan man formalisera som en
gruppegenskap.
Vi inför först en beteckning
ΦT enligt
ΦTp = γpT-T(p)
För varje T är detta ΦT en funktion av p, även
om vi inte satt ut funktionsparenterna
(det brukar inte gruppteoretiker göra)
och det ordnar till varje tänkbart tillstånd p, värdet på
tillståndet T tidsenheter senare. Vi kan nu sammansätta denna
funktion, med den som tar oss ytterligare S tidsenheter framåt
i tiden. Om tillståndet är p vid tiden 0 så är det
ΦS ○ ΦTp
vid tiden T+S. Å andra sidan kan detta också beräknas som
ΦT+Sp
Alltså måste det gälla att
ΦT+Sp =
ΦS ○ ΦTp
Eftersom detta skall gälla för alla p, så måste själva
funktionerna vara lika, dvs.
ΦT+S =
ΦS ○ ΦT
Det är också klart att
Φ0 = id
dvs den identiska funktionen (den som avbildar varje punkt p
sig själv). Man kan se den näst sista ekvationen, som en ekvation
för ett dynamiskt system, med ΦT som tillstånd,
och ΦS som den funktion, som bestämmer
dynamiken. Tillståndsrummet är här ett funktionsrum, och det
oundvikliga begynnelsetillståndet ges av den andra ekvationen.
Annorlunda uttryckt så har vi ersatt ett system med ett
"vanligt" tillståndsrum fyllt av orbits, med ett
system vars tillståndsrum är ett funktionsrum, och med en enda
orbit, som passerar id vid tiden 0.
Funktionerna ΦT tillsammans med
funktionssammansättning bildar en grupp
D = <ΦR,○> för
- Vi har slutenhet, enligt ekvationen ovan, för
ΦT+S tillhör gruppen
- Funktionssammansättning är alltid associativ
- Enhetselementet är Φ0=id, för id
är alltid enhetselementet vid funktionssammansättning
- Inversen till ΦT är Φ-T
För ekvationen
ΦT+S =
ΦS ○ ΦT
kan vi rita ett kommutativt diagram:
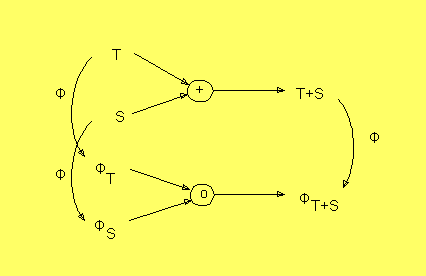
Antag nu att avbildningen från T till ΦT är
inverterbar. Då visar diagrammet en
isomorfism mellan gruppen D och gruppen
<R,+>. I viss mening betyder detta att teorin för
dynamiska system är en trivial teori. Operationen
○ ärver sina egenskaper från +. Den går att göra en grupp av,
den är associativ, kommutativ etc., det måste finnas enhetselement
och inverser osv.
Antag omvänt att avbildningen från T till ΦT
inte är inverterbar. Då finns ett T och ett S+T sådana
att ΦS+T = ΦT. Vi kan skriva
vänsterledet som ΦS○ΦT och
högerledet som id ○ΦT. Därav följer att
ΦS = id.
Då följer också att ΦSΦR =
ΦR för alla R, och det följer för alla tillstånd
i det ursprungliga systemet att ΦSp = p.
Det följer vidare att ΦnS = idn = id
(där mellanledet betyder id applicerat på sig själv n gånger).
Slutligen följer då att ΦnS+T = ΦT.
Man säger att systemet är periodiskt
Ur systemets synpunkt är varje T ekvivalent med nS+T. Detta är
den topologiska egenskapen hos en
cirkel, S1. Vår grupp är
i detta fall strukturellt ekvivalent med gruppen
<S1,+>. Annars är den strukturellt ekvivalent med
truppen <R,+>. Någon tredje möjlighet finns inte.
Dynamiska system och vektorfält
Varje punkt p i tillståndsrummet M passeras av en unik kurva
(orbiten genom p). Om M är en differentierbar mångfald, dvs har
ett tangentrum i varje punkt, så har
också varje kurva, som passerar en punkt en tangentvektor. Detta
gäller då också orbiten genom p. På så sätt kan vi ordna
en vektor X(p) ur TpM till varje p, dvs vi kan bilda
ett vektorfält.
Om M koordinatiseras av koordinatfunktioner xi, så
kan TpM koordinatiseras, genom att varje vektor ges
koordinaterna:
Xi = dxi(γXt)/dt
I det här fallet är kurvan γX given
som orbiten γp. Om vi vänder på denna definierande
ekvation för tangentvektorns koordinater, så får vi
dxi(γpt)/dt =
X(p)i
Detta är en differentialekvation för det dynamiska systemet.
Enligt
satsen om integralkurvor har
denna ekvation lösningar, som är kurvor med de egenskaper
som krävs för orbits till dynamiska system (unika kurvor
genom varje punkt).
Förutsättningen är vissa regularitetskrav på vektorfältets
variation med p. Med M som en differentierbar mångfald och
med regularitetskraven hos X uppfyllda, kan man då komma
från vektorfältet X tillbaka till de orbits som definierar
ett dynamiskt system.
Framställningen av ett dynamiskt system med orbits eller
med vektorfält är alltså under dessa förutsättningar
utbytbara. Man kan representera ett dynamiskt system med
ett vektorfält.
Uttrycket xi(γpt) kan
vi betrakta som värdet av "den fysikaliska storheten"
xi då tillståndet tänkes följa kurvan γp.
Vi kan också uttrycka högerledet som en funktion av samma
"storheter", genom att uttrycka X i koordinaterna xi(p)
med hjälp av en funktion X', dvx
X(p) = X'({
xi(p)
}).
X' är en annan funktion än X, men det är vanligt att man inte
låtsas om detta, utan betecknar X' med X. I så fall skriver vi
dxi/dt =
X({xi
})
Detta är den matematiskt hanterbara formen av differentialekvationen
för ett dynamiskt system.
Begreppet "tillståndsvektor"
I den sista ekvationen är variablerna xi koordinater
för en mångfald.
Men de bildar också tillsammans en tupel, och tupler kan man
alltid se som vektorer i ett
vektorrum. Addition och multiplikation
med skalär är då komponentvis addition och komponentvis
multiplikation med skalär. Frågan är vad dessa operationer betyder
för mångfalden. Givet två punkter p och q på M. De har var sin
tupel av koordinater. Dem kan vi addera komponentvis, och det
ger oss ny koordinater xi(p)+xi(q). Dessa
koordinater ger oss en ny punkt, som vi kan kalla
p +x q, som definierar en addition på M. Men vi
har indexerat additionssymbolen + med koordinatiseringen x,
för resultatet av additionen beror på koordinatiseringen. Det
betyder att additionsregeln för koordinattuplerna inte ger någon
särskild meningsfull operation på mångfalden M.
Vi har egentligen samma situation för det speciella fallet att
mångfalden M är ett vektorrum. Det går alltid att hitta
på koordinatiseringar så att operationen + blir olika för olika
koordinatiseringar. Men om vi koordinatiserar vektorrum på det
vanliga sättet med hjälp av basvektorer, så är det inte så. Då
blir alla +x lika.
En annan sak som kan hända med operationen +x är att
de tänkta koordinaterna för p +x q inte alls pekar
ut någon punkt på M. Vektorrum är lineära rum, vilket betyder
att varje lineärkombination av två vektorer i vektorrummet också
tillhör vektorrumet. Men på en mångfald i allmänhet, finns det
inte ens någon ovedersäglig definition av en "lineärkombination".
Men lineariteten hos ett vektorrum, alltså slutenheten under
lineära operationer, betyder att ett vektorrum måste vara
obegränsat, och det måste inte en mångfald vara.
Ytterligare har mångfalder möjligheten till
topologiska identiteter, som ett
vektorrum saknar.
Av alla dessa skäl bör man inte betrakta tupeln x som en
tillståndsvektor. I ekvationen
dxi/dt =
X({xi
})
är funktionen X i allmänhet olineär. Men tillståndsrummet M
är också olineärt, och det är också viktigt.
Kritiska punkter och deras lokala egenskaper
En kritisk punkt p0 är en punkt där vektorfältet
X är 0 dvs lika med 0-vektorn. Om tillståndet är exakt i
p0 så stannar det kvar där för all framtid. I en
omgivning av p0 kan vi beskriva X med en funktion
X0(p) = X(p-p0)
För X0 gäller att X0(0) = 0. En sådan
funktion kan, om den är tillräckligt reguljär, lineariseras, dvs
approximeras med en lineär funktion, som i sin tur kan skrivas
som en matrismultiplikation med en matris J (Jacobianen):
X0(p) = X(p-p0) = J·(p-p0)
Matrisen J:s egenskaper bestämmer då fältets egenskaper i
närheten av p0. I första hand tänker man sig möjligheten
att diagonalisera J.
I första hand är
man intresserad av egenvärden och egenvektorer, medan själva
diagonaliseringen innebär att man vrider systemet så att
egenvärdena överensstämmer med koordinataxlarna.
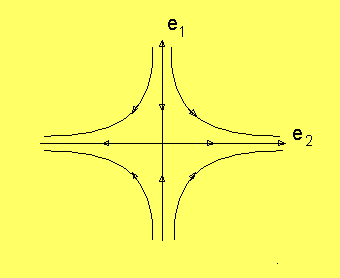
Låt oss först betrakta ett 2-dimensionellt system.
Om J är symmetrisk, och egenvärdena är olika, så är egevektorerna
ortogonala. Vi kan ha den situation som visas här:

I riktningarna e1 och e2 är fältet parallellt
med vektorn (p - p0). Egenvärdena λ är här negativa,
så att fältet pekar tillbaka mot p0. Då säger man att
den kritiska punkten är attraherande. I motsatt fall är den
repellerande. Om egenvärdena har olika tecken, så har
man en repellerande riktning och en attraherande från samma punkt,
och då säger man att man har en sadelpunkt.
Ett egenvärde kan också vara exakt 0. Man kan göra ett
koordinatbyte, så att koordinataxeln x faller längs motsvarande
egenvektor. I variabeln x har då F varken värde eller derivata i
p0.
En Taylorutveckling domineras då lokalt av andragradstermen. Det
betyder att F har samma tecken på båda sidorna av p0.
En möjlighet är då att man har en dipol, som är en sammansmältning
av en attraherande och repellerande kritisk punkt. Orbits ser
ut ungefär på följande sätt:
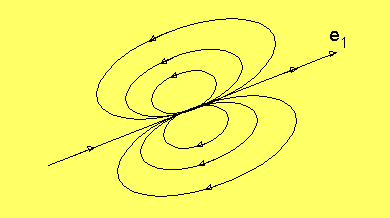
Se även här.
Om båda egenvärdena är lika, så finns det två möjligheter. Den
vanliga är att vi då har egenvektorer i alla riktningar, men
en annan möjlighet är att systemet bara har en egenvektor. I
fallet med egenvektorer i alla riktningar ser systemet
ut som följer:
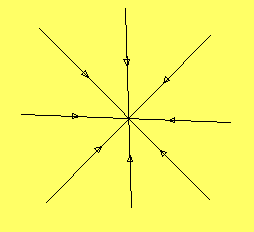
Om J är skevsymmetrisk, så har vi bara rent imaginära egenvärden.
I så fall kan vi genom koordinatbyten få J på formen
Systemet är då en oscillator med orbits som är cirklar runt
p0. Genom en annan koordinatisering blir de ellipser.
Den kritiska punkten kallas ett centrum.

I det allmännaste fallet (varken symmetriskt eller
skevsymmetriskt J) blir egenvärdena komplexa. Då är orbits
spiraler, längs vilka tillståndet rör sig ut från, eller in
mot den kritiska punkten. Den kritiska punkten kallas för
ett fokus.

I tex 3 dimensioner har man liknande situationer. Man kan ha
en punkt som repellerande i ett plan, men attrahernade i den
tredje riktningen. En sådan punkt betraktas fortfarande som en
sadelpunkt. Vad gäller centra och foci, så gäller ju att för en
ekvation med reella koeffecienter, så uppträder rötterna i
komplexkonjugerade par. Samma sak gäller då för egenvärdena
som ju är rötter till en n:e-gradsekvation
sekularekvationen.
Vi kan då ha centra eller foci i ett
plan, men i den tredje dimensionen kan vi inte ha en komplex
rot, utan bara ren attraktion eller repulsion.
Kritiska punkters globala egenskaper
Kritiska punkter kan inte placeras ut godtyckligt i
tillståndsrummet, utan de är underkastade vissa kombinatoriska
eller topologiska begränsningar. Henri Poincaré studerade detta,
speciellt för 2-dimensionella system. Ett verktyg för detta
är så kallade vindlingstal.
Se mera här.
Just för dynamiska system är det lättare att förstå en speciell
faktor här. Attraktorer och repellatorer måste balansera
varandra. Om tillståndet kastas ut från en punkt, måste det
kunna ta vägen någonstans. För ett obegränsat tillståndsrum
kan tillståndet alltid försvinna ut i oändligheten, men i
ett begränsat tillståndsrum måste det kunna gå till en attraherande
kritisk punkt någonstans.
En orbit, som representerar att tillståndet går från en sadelpunkt
till en annan kallas en heteroklinisk orbit. Men tillståndet
kan också går ut i den repellerande riktningen och sedan
närma sig samma sadelpunkt i dess attraherande riktning.
En sådan orbit kallas för en homoklinisk orbit.
Gränscykler
En gränscykel är en periodisk orbit, alltså en orbit som
återkommer till samma punkt efter en viss tid. En gränscykel
är attraherande om orbits i en omgivning av gränscykeln
konvergerar mot gränscykeln. Den är repellerande om
orbits i omgivningen divergerar från gränscykeln. Den kan
också vara attraherande för somliga orbits och repellerande
för andra. Ett sådant fall är då man har en så kallad
sadelgränscykel. Figuren visa en sådan sadelgränscykel.
Orbits, som startar i gränscykelns plan konvergerar i planet
in mot gränscykeln. Orbits som starta över eller under planet
repelleras bort från planet, och därmed bort från gränscykeln.
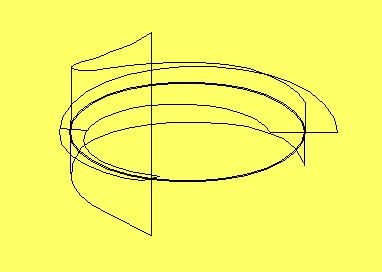
De repellerande och attraherande riktningarna kan också ligga
snett i förhållande till gränscykelns plan. Gränscykeln behöver
heller inte ligga i ett plan.
En gränscykel som varken är attraherande
eller reppelerande kallas neutral. I någon omgivning till
en sådan finns det då orbits, som varken konvergerar eller
divergerar mot gränscykeln. De kan då (men måste inte) vara
neutrala gränscykler.
Lineära system har bara gränscykler om de är Hamiltoninanska
(energibevarande) och de är alltid neutrala. De är orbits kring
en kritisk punkt i origo, som är ett centrum.
Inom mekaniken har man inte lineära system, eftersom Newtons
gravitationslag:
F = G·m1·m2/r2
är olineär. Den celesta mekaniken, där himlakroppar rör sig i
en i stort sett tom rymd, är också Hamoltoniansk. Även där
har man då neutrala gränscykler. T.ex. är
solen omgiven av en oändlig härva av neutrala orbits. Planeter
asteroider och kometer har besatt ett fåtal av dessa orbits.
Planetbanor och kometbanor kan korsa varandra, men det betyder
inte att orbits korsar varandra, för orbits finns i tillståndsrummet
och i tillståndsrummet finns inte bara positionskoordinater
utan också hastighetskoordinater. Banor som möts i samma punkt
har olika hastigheter i den punkten. Naturligtvis innebär ändå
alla dess korsningar en risk för kollision. I själv verket tror
man att planeterna har uppstått ut sådana kollisioner. När
en stor asteroid infångar en liten, så blir de fångade i
varandras gravitation. Banan blir en annan än båda de ursprungligas
men den liknar mest den större asteroidens bana. Möjligtvis kan
det vara så att asteroider som rör sig i cirkulära banor tidigt
hade större sannolikhet för att kollidera med andra. De skulle
därmed gynnas i sin storlekstillväxt, vilket skulle förklara
varför tämligen cirkulära banor dominerar i vårt solsystem.
Om det finns ett dominerande plan där merparten av asteroiderna
finns, är det också en effekt som gynnar storlekstillväxtenen
för asteroider, som finns i detta plan.
Poincaré-sampling
Henri Poincaré studerade gränscykler på samma sätt som kritiska
punkter genom en metod som kallas Poincaré-sampling. Idén var
att sätta upp en plan yta i någon punkt som passerades av
gränscykeln, och studera hur orbits passerade denna yta.
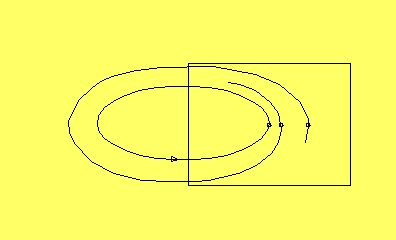
Om gränscykeln är attraherande, kommer de här passagepunkterna
att närma sig gränscykelns skärningspunkt med ytan på samma
sätt som tillståndet närmar sig en attraherande kritisk punkt.
Gränscykler förvandlas alltså till kritiska punkter. En skillnad
är emellertid att vi nu har ett tidsdiskret system; tillståndet
passerar bara ytan vid diskreta tidpunkter. Detta skulle
visa sig få en ganska stor betydelse (ingen länk f.n.)
för Poincaré själv.
Delmångfalder till tillståndsrummet
En orbit γt är självklart en delmängd av
tillståndsrummet och den är en mångfald, för den koordinatiseras
av tiden t. Vi kunde också skriva orbiten med
vår gruppteoretiska notation som Φtp0.
En gränsmängd är ett område där tillståndet vistas vid
stora t. En attraherande kritisk punkt är en gränsmängd, och
den kan definieras som ett gränsvärde
p∞ = limt→∞
Φtp
där p är en punkt, varifrån tillståndet attraheras till den
kritiska punkten. Men det finns gränsmängder, som inte är
punktmängder. En gränscykel är ett exempel. För att då definiera
gränsmängder behöver man göra en liten konstruktion. Låt
I(τ) vara intervallet τ<t<∞ i variabeln t.
Efter tiden τ befinner sig tillståndet i mängden
ΦI(τ)p
där vi har satt in en mängd I(τ) som argument i funktionen
Φ (se här). Vi kan då se gränsmängden
som ett gränsvärde
ω(p) =
limτ→∞ ΦI(τ)p
Detta är den gränsmängd tillståndet hamnar i om det startar i
p. Gränsvärdeskonstruktionen behöver formaliseras en smula.
För att få en diskret mängd mängder ersätter vi τ med
ett heltal i. Sedan inför vi en slutningsoperator för en mängd
som tillfogar randen till mängden:
cl(M) = M ∪ ∂M
Då kan vi bilda gränsmängden genom en oändlig serie mängdskärningar:
ω(p) = ⋂
i=0∞
cl(ΦI(i)p)
Begreppet Inmängd bildar man som en invers till
funktionen ω. Givet en gränsmängd Ω, från vilka punkter
når man Ω? Svaret är
In(Ω) = ω-1(Ω) =
{p
|ω(p) = Ω
}
Man kan göra samma sak för en godtycklig mängd L. In(L) är
mängden av punkter, som leder till en gränsmängd, som finns i L.
In(L) =
{p
|ω(p)
⊆ L
}
En inmängd (som är en delmångfald av tillståndsrummet) kallas
en attraherande mångfald om dess inmängd bara är något
större än den själv. Formellt betyder "något större" att man
kan skjuta in en öppen mängd, U, mellan L och dess inmängd, så att
L ⊂
U ⊂
In(L)
Om L är en attraherande mångfald, så kallas In(L) också
för bassängen till L.
När två bassänger möts, kallas deras gemensamma rand för
en separatris. Om tillståndet befinner sig i en
separatris, så kan det inte lämna separatrisen, för det
kan inte välja att gå in i den ena bassängen men inte den
andra. En separatris måste därför vara uppbyggd av orbits.
En attraherande mångfald kallas en attraktor om den
är transitiv. Det betyder att den rymmer orbits (minst en),
som fyller ut den helt och hållet. Varje öppen delmängd av
attraktorn passeras av minst en orbit, som sedan passerar
alla andra öppna delmängder av attraktorn. Detta är också
en slags odelbarhetsegenskap, som innebär att man inte kan
klippa sönder en attraktor utan att klippa av orbits.
Attraktoregenskapen är trivial för t.ex. en attraherande
gränscykel. En orbit som startar någonstans längs gränscykeln
kan inte undgå att fylla ut gränscykeln helt och hållet.
Attraktoregenskapen är icke-trivial först då attraktorn är
något större än en kurva, t.ex. en yta. Då kan transitiviteten
betrakta som en tolkning av begreppet "komplext system". Systemet
är komplext genom att det är odelbart.
Alla dessa begrepp har motsvarigheter då vi låter tiden gå
baklänges. Man talar om gränsmängder även i bakåtgående tid, men
de betecknas med α(p), och är alltså det område varifrån
tillståndet en gång måste ha kommit, om det nu är i p. Ett
α har en utmängd, dit tillståndet kan gå från α.
Det finns repellerande mångfalder och de kallas
repellatorer om de är transitiva.
Det följer av definitionen att man inte kommer in i en
inmängd. Man måste ha varit där hela tiden. Man kommer inte
heller ut ur en utmängd. Man är där för alltid. Det
betyder att om tillståndet rör sig från en gränsmängd α
till en gränsmängd ω, så är den hela tiden i
skärningen mellan Out(α) och In(ω), och denna skärning
måste finnas.
Utmängden till en sadelpunkt i två dimensioner är en enda orbit.
Inmängden till
en sadelpunkt är också en enda orbit. Om vi har en homoklinisk
orbit, dvs en orbit som går från sadelpunkt till samma
sadelpunkt, så måste in och utmängden sammanfalla. Dvs
det måste se ut så här:
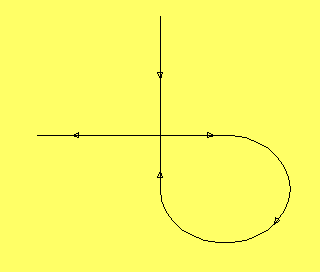
Det kan inte se ut så här:
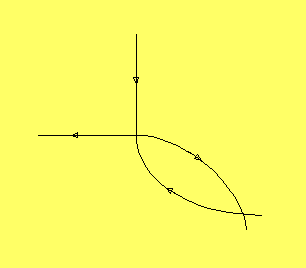
Det framgår i och för sig redan av att orbits inte får korsa
varandra.
Invarianta mångfalder
En invariant mångfald, M, definieras så, att om tillståndet kommer
in i M, så blir det sedan för alltid kvar i M. Man kan uttrycka detta
så:
ΦI(0)
⊆M
där som tidigare I(τ) är intervallet τ < t < ∞.
Den "framtida delen" av en orbit, dvs
ΦI(0)p
är en invariant mångfald, för
ΦI(0)M = ΦI(0)○
ΦI(0)p = ΦI(0)+I(0)p =
ΦI(0)p = M
Observera alltså att I(0)+I(0) = I(0); de är båda intervallet
från 0 till ∞.
En gränsmängd är en invariant mångfald, eftersom den är en
framtida del av en orbit.
En bassäng är en invariant mångfald, för om tillståndet skulle
kunna lämna bassängen, så skulle den vara på väg mot en ny
attraktor, men själva varandet i en bassäng betyder just att
man skall vara på väg just mot den bassängens attraktor och inte
någon annan.
På samma sätt kan tillståndet inte heller lämna en separatris, dvs
gränsen mellan två bassänger, för att ge sig ut i endera bassängen.
Varje sammanhängande område av separatriser är därmed en
invariant mångfald.
Man kan göra sig en "syntetisk" invariant mångfald med hjälp
av en så kallad
Lyapunov-funktion. Det är en reellvärd funktion f av
tillståndet, som konstruerats så att
df(p)/dt ≤ 0
då systemet följer sin dynamik. Mängden Mc enligt
Mc = { p
|
f(p) < c
}
är då en invariant mångfald, för tillståndet kan inte från
Mc ta sig till ett område med större c, eftersom f(p)
hela tiden minskar. Om Mc består av flera åtskilda
komponenter, så är var och en av dem för sig en invariant mångfald.
För ett i övrigt slutet fysikaliskt system med värmeförluster till
omgivningen, fungerar den totala energin som en Lyapunov-funktion.
Lyapunov själv skall ha sett sin funktion som en generalisering
av totalenergin.
Begreppet invariant mångfald kan användas för riskanalys. Om Z
är ett område som innebär fara, och om vi har en invariant
mångfald M, som inte skär Z, så kan vi utan risk släppa iväg
systemet från starttillstånd, som ligger inuti M.
Stabilitetsanalys är ett exempel på detta.
Då är Z ett område med stora
koordinatvärden, som sträcker sig ut i oändligheten i
koordinatrymden.