Nedanstående diagram är ett så kallat kommutativt diagram, eller ett diagram som kommuterar:
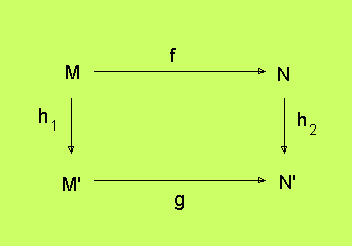
Idén med diagrammet är att man skall komma till samma resultat oavsett vilken väg genom diagrammet man tar. Om man startar med ett element x ur M, och går den övre och högra vägen, eller den vänstra och nedre, så skall resultatet bli detsamma. Det betyder alltså att
h2○f(x) = g○h1(x)Eftersom detta skall gälla för alla x, så är det funktionerna som är lika, så då skall vi hellre skriva:
h2○f = g○h1Om nu h1 och h2 båda är inverterbara funktioner, så säger vi att vi har en isomorfism, och att den övre och nedre delen av diagrammet är isomorfa. Varje element i M har exakt en motsvarighet i M' och tvärtom, och det samma gäller för N och N'. I själva verket har också f en motsvarighet i det enda g, som är möjligt på platsen. Om vi utnyttjar det kommutativa diagrammet från M' till N', så ser vi att
g=h2○f○h1-1En annan syn på isomorfismer, är att de båda världarna, den övre och den nedre, inte bara är utbytbara. De är identiska. De är identiska, men någon har försökt lura oss att tro något annat, genom att döpa om elementen i den ena av världarna. Mycket följer i alla fall av isomorfismer. Det som är isomorft med en grupp, är en grupp. Det som är isomorft med ett vektorrum är ett vektorrum och så vidare.
Funktionerna f och g kan naturligtvis ta flera argument. Här har vi två operationer (alltså funktioner med två argument) och en isomorfism mellan dem, som heter f.
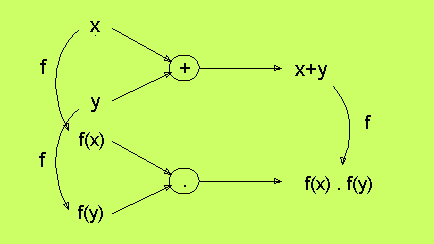
Funktionen f överför alltså operationen + till operationen ·. Om + är vanlig addition av reella tal, och · är vanlig multiplikation, så är f en exponentialfunktion. Dess invers är nyttigare i det här sammanhanget, eftersom den överför multiplikation, som anses svårare, på addition. Inversen är förstås logaritmen.