Stokes' sats

Stokes' sats:

∫_Mdω = ∫ _∂Mω

#

Båda led är integraler av differentiella former, en n-form ω och en n+1-form dω, som är differentialen av ω. Integrationen sker över områdena M och ∂M, dvs över randen av M.

Stokes' sats gäller bara under förutsättning att M är en orienterbar mångfald. Den gäller därmed inte på t.ex. ett Möbiusband.

Stokes' sats innehåller Green's, Gauss's och Stokes' formler som specialfall.

Samtidigt är satsen modersats till en hel gren av matematiken, kallad algebraisk topologi. Bakgrunden till detta är följande tänkbara situaton. Antag att man kan visa att ω är sådan att dω = 0. Antag att γ är en sluten kurva, eller ett annat slutet simplicialt komplex, t.ex. en sluten yta. Antag nu man finner ett fall där

∫_γ ω ≠0

Om γ vore en rand ∂M till en mängd M, så skulle detta innebära en orimlighet, för Stokes' sats skulle då ge:

∫_γω = ∫_M0 = 0

Vi har därmed bevisat att γ inte är en rand. Det betyder att γ innehåller ett hål.

Man brukar säga att en integral är bilineär, så att

∫_Mω₁ + ω₂ = ∫_Mω₁ + ∫_Mω₂

men också så att

∫_M₁+M₂ω = ∫_M₁ω + ∫_M₂ω

Vad som menas med "+" mellan mängder är emellertid en smula komplicerat. Om alla mängder är disjunkta, så + samma som union. Om mängderna är kurvor, så måste man hålla reda på orientering. Om vi går fram och tillbaka längs samma kurva så försvinner integralen, men om vi passerar en kurva 2 gånger i samma riktning, så fördubblas bidraget från integralen.

Exempel: Funktioner från C till C

Låt ω vara f(z)·dz, där f är en funktion från C till C. Uttrycket går att utveckla i komponenterna av de komplexa talen f och dz som:

fdz = (g+ih)(dx+idy) = (g+ih)dx + (ig-h)dy

Detta är en differentiell 1-form i dx och dy. När vi differentierar får vi definitionsmässigt

dω= d(g+ih)∧dx+ d(ig-h)∧dy

d(g+ih) kan vi utveckla enligt kedjeregeln i dx och dy. Då får vi termer som dx∧dx och dy∧dy, som försvinner, och vi har att dy∧dx = -dx∧dy. Det ger

dω = (-(∂g/∂dy+∂h/∂x) + i(-∂h/∂y+∂g∂x)) dx∧dy

Men om funktionen f är deriverbar från C till C så följer av Cauchy Riemanns ekvationer att detta är 0, alltså dω=0. Att f är deriverbar, dvs tillhör deriverbarhetsklassen C¹, medför, som vi strax skall, att den också tillhör den mindre deriverbarhetsklassen C^ω, dvs att den är analytisk, och detta är då den vanliga termen för att beteckna deriverbara funktioner från C till C.

Låt nu C' vara mängden av punkter i C, där f är analytisk. I hela C' gäller att dω=0, Om vi därför hittar en sluten kurva γ i C', sådan att

∫_γω ≠ 0

så betyder det att kurvan γ omsluter ett hål i C', alltså ett område där f inte är analytisk.

Speciellt är polynom analytiska överallt, och rationella funktioner (kvoter mellan polynom) är analytiska överallt utom i nämnarens nollställen. Sådana nollställen kan alltså lokaliseras med den här metoden. I sin tur spelar rationella funktioner rollen som överföringsfunktioner för dynamiska system (lineära, tidsinvarianta och ändligtdimensionella).

Cauchy's integralformel

Följande integrationsformel gäller:

∫_{C_a} dz/(z-a) = 2πi

där C_a är en liten cirkel som omsluter punkten a. Funktionen f's roll spelas här av funktionen 1/(z-a). Den är analytisk överallt utom i a, och det är därför som integralen längs en kurva, som just omsluter a kan bli ≠0. Nu kan man bilda en sluten kurva, μ, som inte innehåller a på följande sätt:

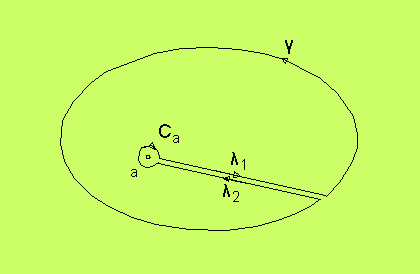
Vi har för integralen längs hela denna kurva att

∫_μω = ∫_{C_a}ω + ∫_λ₁ω + ∫_γω + ∫_λ₂ω = 0

De båda integralerna längs λ₁ och λ₂ tar ut varandra. Vänder vi på orienteringen, så att γ får samma orientering som C_a, så får vi

∫_γω = ∫_{C_a}ω

Detta gäller alltså för alla kurvor γ som omsluter a. Betrakta nu följande integral:

1/2πi ∫_γ f(z)/(z-a)

där f är en överallt analytisk funktion. Vi kan skriva om den som

1/2πi(∫_{C_a}f(a)/(z-a)dz + ∫_{C_a}(f(z)-f(a))/(z-a) dz)

Den andra temen innehåller en differenskvot som går mot en ändlig derivata överallt på C_a om f är en analytisk funktion. Då integrationsområdet går mot 0, om vi låter radien hos C_a gå mot 0, så försvinner den termen. I den första termen är f(a) en konstant, som vi kan bryta ut ur integralen. Då får vi:

Sats: (Cauchy's integralformel)

f(a) = 1/2πi∫_γf(z)/(z-a)dz

#

Satsen säger alltså att man kan räkna ut f's värde i en godtycklig punkt a, om man bara känner f's värden längs en kurva, som omsluter a.

Analyticitet

Funktionen 1/(z-a) är värdet av en oändlig geometrisk serie, och den kan alltså skrivas som en potensserie i a. Med hjälp av Cauchy'integralformel kan man då teckna f(a) som en potensserie i a. Den potensserien kan inte vara annat än Taylorserien för f, och därmed måste alla derivator hos f existera, och därmed kan man teckna Taylorserien, och man vet att den konvergerar mot f. Därmed tillhör f deriverbarhetsklassen C^ω, dvs den är analytisk.

Liouvilles teorem

En potensserie f(a) måste gå mot ∞ då a går mot ∞. Varje term för sig måste gå mot ∞, och olika termer kan inte ta ut varandra, för för tillräckligt stora a måste den n:e termen dominera över den n-1:a. Ett undantag gäller naturligtvis för den 0:e termen, som är konstant. Detta leder till:

Sats: (Liouville's teorem) Den enda överallt analytiska funktioner som är begränsad, är den konstanta funktionen.

#

Algebrans fundamentalsats

Algebrans fundamentalsats säger att en n:e-gradsekvation, p(z) = 0, har minst en rot om n>0. Om man nu har hittat denna rot som r₁, så kan man dividera ut (z-r₁) ur p(z). Då får man en n-1:gradsekvation och den har också minst en rot, om inte gradtalet nu har sjunkit till 0. På så sätt finner man att en n:e-gradsekvation har n rötter, men genom den här forumuleringen har man undvikit problemet att flera rötter kan sammanfalla.

Beviset utnyttjar en reduktion till en motsägelse samt Liouville's teorem. Antag alltså att p är av grad n>0 och att ekvationen p(z)=0 saknar rötter. Då är 1/p(z) analytisk överallt, för en rationell funktion är analytisk överallt utom i nämnarens nollställen. För z långt från origo är 1/p(z) ≈ 1/zⁿ, som går mot 0 långt från origo. Funktionen är alltså begränsad långt från origo, och den är begränsad nära origo också, eftersom p(z) ≠ 0. 1/p(z) är alltså analytisk och begränsad, och enligt Liouville's teorem är den då konstant, och då är också p(z) konstant, vilket strider mot förutsättningarna.

Exempel: Vindlingstal

Det komplexa talplanet C är ju geometriskt samma sak som det vanliga talplanet R², men det är försett med extra algebraiska strukturer, som gör att man kan definiera differenskvoter och derivator, och införa en klass av deriverbara funktioner. Den klassen är i själva verket ganska liten, vilket framgår av Cauchy-Riemanns ekvationer. För den klassen kan man utnyttja Stokes' sats.

Men det går att göra en teori som kan användas för att analysera funktioner från R² till R² i allmänhet. Sådana funktioner kan man tolka som vektorfält över R². I F(x) pekar de två koordinaterna av x ut en punkt. De två koordinaterna av F(x) representerar en vektor, och vi låter den "börja" i punkten x. Annorlunda uttryckt så tolkar vi vektorn som en ekvivalensklass av riktade sträckor, och som representant för klassen väljer vi den riktade sträcka, som börjar i x. Detta ger oss den vanliga föreställningen om ett vektorfält. Tangentrummet T_pR² till R² är i varje punkt R², och det gör att detta vektorfält faller inom ramen för den "officiella" definitionen av ett vektorfält.

Låt vidare γ vara en sluten kurva i R². Vid parametervärdet t passerar den en punkt x = γ_t. Där har vektorfältet värdet F(γ_t). Om vektorn inte har beloppet 0, så har den en riktning där, som vi kan ange genom en vinkel Θ. Nu inför vi en differentiell form ω_Θ enligt

ω_Θ = dΘ

Vi har enkelt att

dω_Θ = ddΘ = 0

Nu har vi det problemet att att Θ såsom vinkel inte är entydigt bestämd, utan är likvärdig med varje vinkel Θ+2nπ. Om vi gör Θ entydig genom att t.ex. stänga in den i intervallet från 0 till 2π, så blir vår funktion Θ(t) = Θ(F(γ_t)) diskontinuerlig då vi passerar en punkt där Θ går förbi 0 i negativ riktning, eller förbi 2π i positiv riktning. Därför släpper vi på kravet att Θ(t) skall vara en funktion, genom att välja bland olika möjligheter till värde på Θ efter omständigheterna. Då vi passerar värdet 2π i positiv riktning, låter vi Θ fortsätta förbi 2π, och då vi passerar värdet 0 i negativ riktning låter vi Θ gå ner till negativa värden. Då får vi Θ(t) som kontinuerlig, så att differentieringen är möjlig, men Θ(t) är strängt taget inte längre en funktion. Å andra sidan baseras överläggningen dω_Θ = ddΘ = 0 bara på lokala egenskaper hos Θ(t). Detta är naturligtvis en smula tvivelaktigt, och det går att utvecklar en mera vattentät teori, men den blir betydligt krångligare.

Vi har alltså dω_Θ = 0, överallt utom i de punkter där vektorfältet F(x) = 0. Vi kallar den del av R² där F(x) ≠ 0, för Z. För varje γ, som är en rand ∂A till ett område A i Z, gäller att

∫_γ ω_Θ = ∫_∂A ω_Θ = ∫_A dω_Θ = 0

Om alltså för något γ vi har att

∫_γ ω_Θ ≠ 0

så vet vi att kurvan måste omsluta ett hål i Z, så att den inte kan vara rand till något A i Z. Med andra ord så innesluter kurvan ett nollställe hos vektorfältet F.

Man kan inse att integralen måste ge ett värde av formen 2πk, är k är ett heltal. Talet

W(F,γ) = (1/2π) ∫_γ ω_Θ

kallas vindlingstalet för fältet F runt kurvan γ. Rent bildligt anger det hur vektorn F(γ_t) snurrar runt, då vi rör oss runt kurvan. För att kunna diskutera tecknet på W, inför vi konventionen att kurvan γ genomlöps medsols. Genomlöper vi den i motsatt riktning byts tecknet.

Nollställen till F uppträder vanligen som isolerade punkter. Om vi lägger γ snävt runt en sådan punkt, så att den inte omsluter några andra nollställen, så kallas W(F,γ) för nollställets index. Index ger en viss information om fältet ser ut runt nollstället. Om vi lägger en kurva runt flera nollställen, så är det lätt att visa att vindlingstalet ger summan av deras index.

Figurerna visar ett vektorfält med ett nollställe.

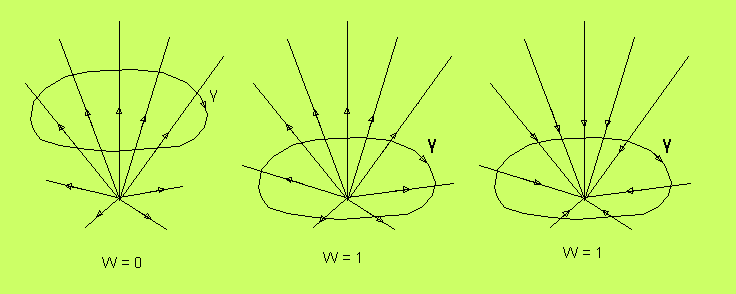
I den vänstra figuren ligger kurvan utanför nollstället. Då är vindlingstalet 0. I den mellersta figuren innesluter kurvan nollstället. Då blir vindlingstalet 1. Vektorfältet är här repellerande ut från nollstället. I den högra figuren har vi vänt fältet, så att det är attraherande mot nollstället. Vindlingstalet blir fortfarande 1. Vindlingstalet kan alltså inte skilja på attraherande och repellerande nollställen.

Figurena nedan visar två andra typer av nollställen

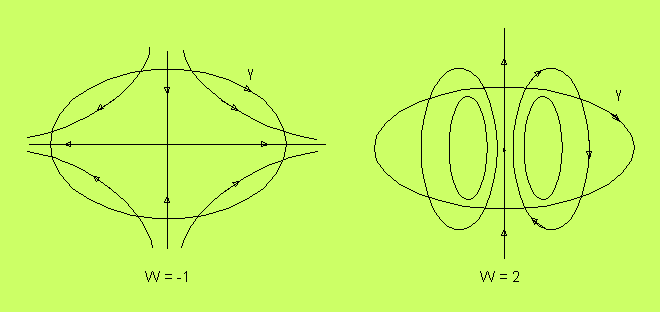
Den vänstra figuren visar en så kallad sadelpunkt, som är attraherande i vertikal riktning och repellerande i horisontell. Den har W = -1, vilket karakteriserar sadelpunkter. Den högra figuren visar en dipol. Den kan ses som ett gränsfall där ett attraherande och repellerande nollställe närmar sig varandra. Längs den vertikala linjen är fältet hela tiden uppåtriktat men beloppet sjunker till 0 i nollstället. Här blir W = 2, vilket det bör vara, eftersom det är ett gränsläge där vi utgått från två nollställen.

Stokes' sats gäller ju på alla orienterbara mångfalder. För teorin för vindlingstal finns det en svårighet att skapa en referensriktning mot vilken vi kan mäta vektorfältets riktning som vinkeln Θ. Men vi har ju en koordinatisering, och vi har alltid i varje punkt en kurva som bildas, då vi låter den första koordinaten variera, medan de övriga står stilla. Vi kan (exempelvis) mäta Θ relativt tangenten till den kurvan. Då kan vi ta över teorin till alla tvådimensionella orienterbara mångfalder. För mångfalder som saknar rand (alltså är slutna) och som är begränsade, finns en intressant sats av Poincaré. Den säger att summan av index för alla nollställen måste vara =

χ = h₂ - h₁ + h₀

Idén är här att man kan deformera mångfalden så att den blir kantig, och får plana ytor, raka kanter och distinkta hörn. h₂ är antalet plana ytor efter denna deformering. h₁ är antalet raka kanter och h₀ är antalet distinkta hörn. Dessa tal blir olika för olika deformationer av mångfalden, men kombinationen χ av dem är en invariant, som får samma värde för alla tänkbara deformationer. En sfär kan på detta sätt deformeras till en kub, och räknar man igenom ytor, kanter och hörn på en kub, så blir χ = 2. Summan av index för alla nollställen skall alltså vara 2. Det betyder att ett vektorfält på en sfär inte kan sakna nollställen. Detta resultat är känt som en sats om konsten att kamma en kokosnöt. Om nollställena är repellerande eller attraherande, så har de i båda fallen index 1, så vi kan ha två sådana nollställen. Man kan inse att det ena av dem måste vara repellerande och det andra attraherande. Genom att föra in sadelpunkter, får vi negativa bidrag, och det öppnar möjligheten att föra in fler attraherande och repellerande nollställen. Men lärdomen av detta är att man inte kan föra in nollställen hur som helst på en mångfald. Det kan man inte i R² heller.

Storheten g, som kallas en mångfalds genus är antalet hål genom mångfalden. En torus har genus 1. Man kan göra en kringla med 2 hål, osv. Nu finns det en sats som säger att χ = 2 - 2g. För en torus är då χ = 0. På en torus kan man alltså ha ett nollställefritt vektorfält. Men om man någonstans vill ha ett attraherande eller repellerande nollställe, så måste man också införa någon sadelpunkt för att få ner index till 0. Sedan måste man också ta hänsyn till balansen mellan attraktion och repulsion i ett fält.

Vektorfält över 2-dimensionella mångfalder bestämmer dynamiken för dynamiska system med dessa mångfalder som tillståndsrum. Henri Poincaré använde därför begreppet vindlingstal för att analysera sådana dynamiska system.

till innehåll