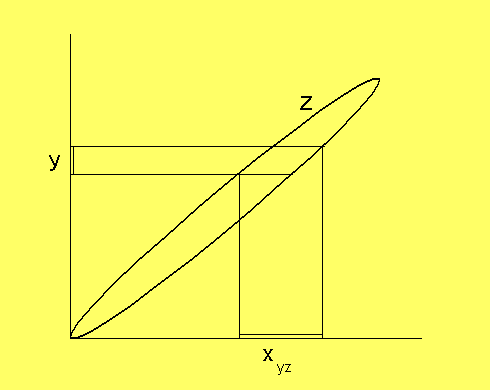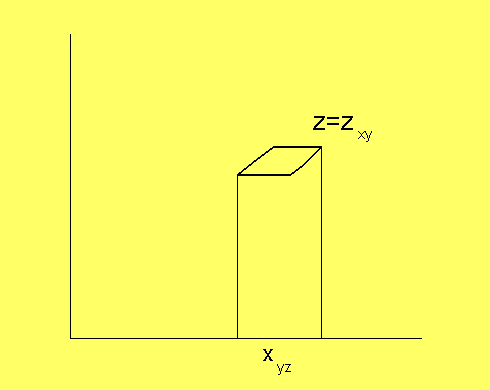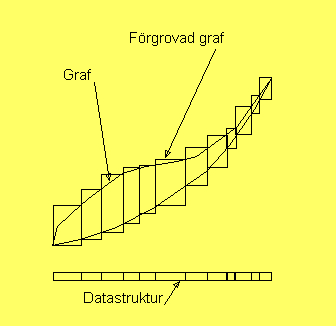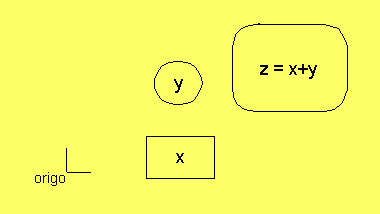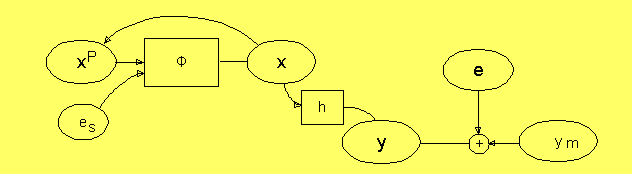Relationsnätverk

Innehåll

Definition
Transport och unifiering
Representation av osäkerhet
Exempel på relationer
Cartesisk produkt
Grafrelationen
Summarelationen
Translationsrelationen
Tidsuppdatering
Mängdrepresentation
Bildrepresentation
Språket Retina
Relationer i Retina
Bildrelationer i Retina
Instruktioner i Retina
Exekvering av Retina
Exempel

Definition

Ett relationsnätverk är ett nätverk med noder och relationer, som t.ex.

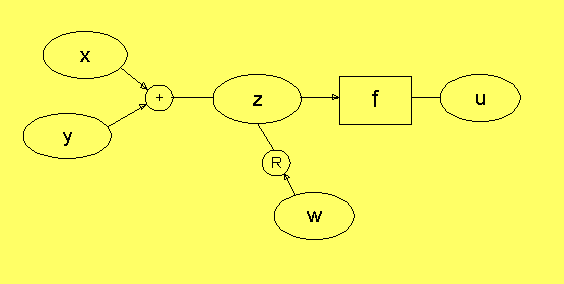
x,y,z,u,w är noder, som representerar värdet av olika "storheter" eller "variabler", och som också representerar osäkerheten om dessa värden.

+, R och f är relationer mellan dessa värden. Relationen + kan betyda att:

z = x + y

Pilarna vid +-symbolen anger vilka värden som går in i summan. Den pillösa linjen markerar resultatet av summan. Det här är en ternär relation (en relation mellan 3). Relationen f betyder att

u = f(z)

dvs här har vi en relation som uppfyller kraven på en funktion (entydig u som uppfyller relationen för varje tänkbart z). f ger en binär relation (en relation mellan 2). R är en allmän relation (binär) som skrivs

wRz

Vänsterelementet i den här notationen motsvarar en pil vid R

Transport och unifiering

Givet någon information om ett värde (i form av en representation om osäkerheten om värdet) och givet en relation med en grannod. Då kan man säga något om värdet på grannoden. Denna process kallas transport, och man säger att man lägger ett bud på värdet hos grannoden.

Om en nod är kopplad till flera grannoder via relationer, kan det på det här sättet komma flera bud på nodvärdet. Dessutom kan det i noden själv finnas ett a-priori-bud på nodvärdet. Det kan då uppkomma en förhandling där man försöker finna ett uttalande som alla buden (budgivarna) kan enas om. Denna process kallas unifiering.

Efter unifieringen respekteras resultatet av förhandlingen av det omgivande nätverket, och resultatet kan nu transporteras vidare till andra noder, eller tillbaka till budgivarna. På så sätt sprids information genom nätet, och genuint ny information skapas när information möts från olika håll. Det finns en slags "Huygens princip" för information.

Givet en relation mellan x och y, så kan man alltid lägga ett bud på x, givet y, och man kan alltid lägga ett bud på y givet x. All möjlig trafik i ett relationsnätverk är därför dubbelriktad. Förbindelsen mellan noder är alltid ömsesidig. Detta hänger samman med den symmetriska naturen hos relationer. En relation är inte "från-till" utan "mellan". Om en relation beskrivs av en funktion, så kan man transportera information genom funktionen men också genom funktionens invers.

Representation av osäkerhet

Osäkerheten om nodvärdet i en nod kan representeras på olika sätt. Det tre mest närliggande är

som stokastiska variabler
som mängder
med logiska predikat

Stokastiska variabler representeras i sin tur med hjälp av sannolikhetstätheter, och transport och unifiering blir operationer på dessa sannolikhetstätheter. Detta finns beskrivet här [pdf].

I mängdrepresentationen, finns i varje nod en mängd. Om mängden X finns i noden x, så betyder det utsagan

x ∈ X

Transport genom funktioner ges genom att applicera funktionen på mängden X. Om alltså relationen är y = f(x) och noden x rymmer mängden X, så blir budet Y_X på y:

Y_X = f(X)

Motsvarande kan göras för till exempel addition

Z_XY = X + Y = {x + y | x ∈ X ∧ y ∈ Y }

För den allmännare binära relationen xRy har vi ett bud X_Y som

X_Y = { x | ∃ y ∈ Y : xRy }

Unifiering är mängdskärning.

Representationen med predikatlogik, innebär att det i varje nod finns ett predikat, dvs en funktion P, som avbildar varje tänkbart x-värde på sant eller falskt. Om P(ξ) är sann, så är ξ ett möjligt värde på x. Predikatrepresentationen överförs på mängdrepresentationen genom följande avbildningar

Givet X. Då är P(x) = (x ∈ X)
Givet P. Då är X = { x | P(x) = sann }

I fortsättningen beskrivs mängdrepresentationen, och mängderna i noderna ges samma namn som variablerna (dvs t.ex. små bokstäver).

Exempel på relationer

Cartesisk produkt

Givet två värden ξ och η ur två mängder, x och y, så finns det en parbildningsoperation, som ger paret (ξ,η). Mängden av alla par, som man kan bilda på detta sätt kallas den Cartesiska produkten mellan x och y och betecknas x × y:

x × y = { (ξ,η) | ξ ∈ x, η ∈ y }

Man kan se den Cartesiska produkten som att man applicerar parbildningsfunktionen (,) på mängder. Symboliskt

× = (,)_s

Den Cartesiska produkten används för att bygga upp rum av högre dimensioner ur rum av lägre, t.ex. ett rum av ett golv och en höjd.

Den Cartesiska produktens invers är en projektion ner på rum av lägre dimension. Givet en mängd z och en mängd y och relationen z = x × y. Vad är budet på x ? Det korrektaste svaret är: Mängden av alla vänsterelement ur sådana par ur z, som har högerelement, som finns i y.

x_zy = { ξ | ∃(ξ,η) ∈z, där η ∈ y }

Grafiskt kan det se ut på följande sätt:

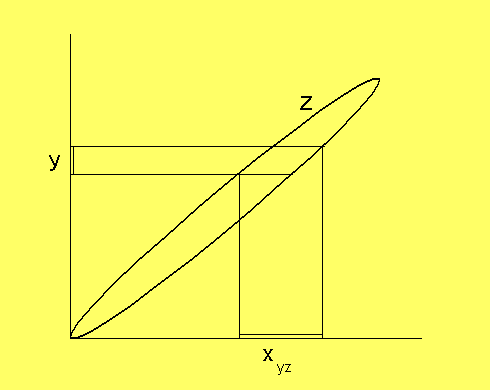
Praktiskt behöver man inte göra unifieringen på detta sätt. Man kan utelämna kravet på att högerelementet i z måste tillhöra y. Då måste man först unifiera z från y och x och sedan x från z:

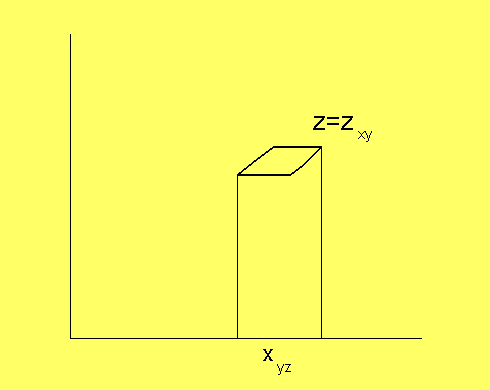
Observera att mängden z i de här figurerna inte skulle kunna uppstå som en Cartesisk produkt. En sådan mängd måste vara rektangulär. z måste komma från en annan del av nätet.

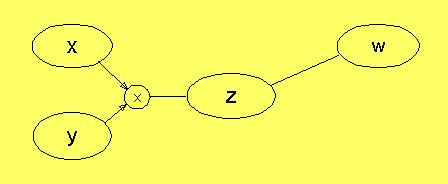
Om vi projicerar z på x och y, och sedan transporterar x och y tillbaka till z, så händer ingenting, för z har kvar sitt värde, och det blir kvar efter unifieringen, som är en mängdskärning. Men i det här nätet är processen att gå från z till z' informationsförstörande:

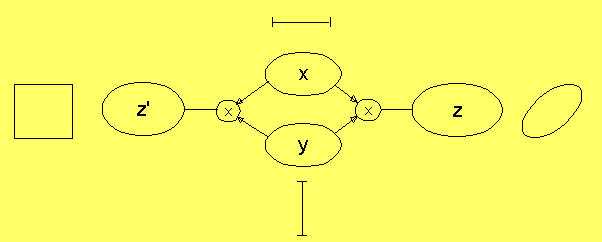
Den Cartesiska produkten avbildar den tomma mängden på den tomma mängden. Antag att

z = x × y

och att x = ∅. z är då mängden av alla par bildade av ett element ur x och ett element i y. Men det finns inga element i x, och därför finns det inga par i z. Efter unifiering först till z och sedan till y, finns det inga element i y heller, dvs y = ∅.

Grafrelationen

Grafen för en relation definieras av:

Graf(R) = {(x,y) | xRy }

alltså mängden av par (x,y) av x och y, som uppfyller relationen. I ett relationsnätverk är en relation implicit definierad av att man pekar ut 2 noder. Givet detta så kan man då beräkna grafen för den relationen och placera den som en mängd av par i en nod. Detta representerar en förbindelse mellan två skilda världar i ett relationsnätverk; dess noder och dess relationer. Sedan grafen bildats kan man använda den för att på nytt generera relationen genom att projicera grafen på en x-nod och en y-nod:

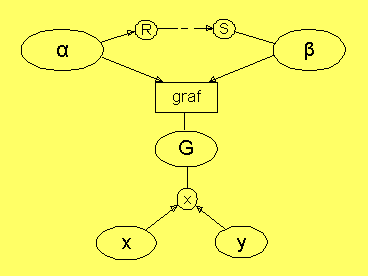
I praktiken måste man göra två tillägg till den här beskrivningen.

Man måste närmare definiera kedjan av relationer mellan α och β som skall konstituera relationen. Annars kan ett oavsiktligt tillägg till nätet av nya relationer ge icke önskade resultat
En graf är i många fall en mycket informationsrik struktur, som kan kräva oändligt många data. Därför är det nödvändigt att göra en förgrovning av grafen, vilket innebär att grafen täcks av ett ändligt antal rektangulära områden.

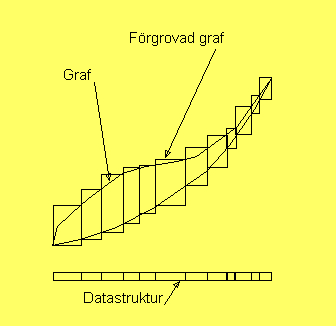
För att styra förgrovningen förser man först noden α med datastrukturen i den nedre delen av figuren, alltså en uppsättning eller lista av intervall. Om relationen kan beskrivas som en funktion, f, alltså om β = f(α), och noden α är laddad med intervall α_i, så ges budet på den förgrovade grafen av

G_αβ = ⋃_i (α_i × f(α_i))

Summa-relationen

Om vi har relationen

z = x + y

och noderna innehåller mängderna x och y, så blir budet

z_xy= { ξ + η | ξ ∈ x, η ∈ y }

En förutsättning för att detta skall vara definierat är att elementen ξ och η går att addera. I allmänhet antar vi att detta är möjligt genom att de är medlemmar i ett vektorrum, dvs x och y är delmängder av vektorrum. I själva verket måste ju ξ och η vara medlemmar i samma vektorrum, och då t.ex. vara vektorer av samma dimension. Addition innebär en ökning av osäkerhet. Om det finns en osäkerhet både i x och y (så att varken x eller y är punktmängder), så blir osäkerheten om z ännu större. Figuren visar en summarelation mellan tre storheter i ett 2-dimensionellt vektorrum

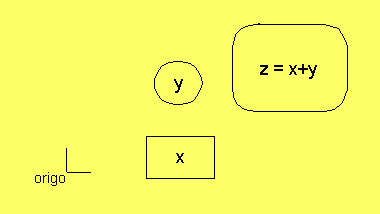
Inversen till summa är differens. Differensen ökar också osäkerheten. Ur relationen z = x + y, kan vi lösa x = z - y, som kan skrivas x = z + -y. Detta är fortfarande addition, men med y speglat i origo. Om z och y givna enligt föregående bild får vi följande bild av budet på x:

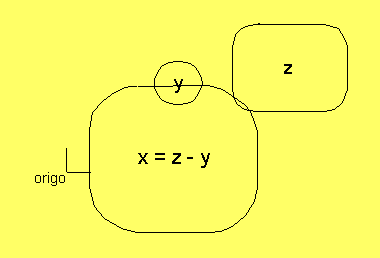
Translationsrelationen

Relationen translation, skriven

x + y ⊆ z

definieras av följande bud på x:

x_zy = { ξ | ξ + y ⊆ z }

Med ξ + y menar vi här translation av mängden y (som är en delmängd av ett vektorrum) med vektorn ξ (vi kunde också skriva det med samma mängdnotation som tidigare som {ξ } + y). x är allltså mängden av alla vektorer ξ sådana att y translaterat med detta ξ får plats i z. Här uttrycker y och z vanligtvis inte osäkerhet utan form. Det resultat vi får i x kan däremot uttrycka osäkerhet. Den vanliga användningen av relationen är att leta efter något som liknar y i en värld z. x ger oss positionen, men om x inte är en punktmängd, så har vi en osäkerhet om positionen hos det funna objektet. I världen z kan det också finnas flera "y", och i så fall blir x en mängd av flera åtskilda positioner. Eftersom y är en bekskrivning av något som vi letar efter, kallar vi y för en specifikation. Translationsrelationen är symmetrisk i x och y, och det är godtyckligt vilken av noderna x och y man låter vara specifikation, och ur vilken nod man tar ut resultatet. Man kan inte hitta ett föremål i z, som ser ut som y men är mindre än y med den här relationen. I så fall får man börja med först förstora mängderna i z genom att addera en storleksosäkerhet. Följande figur visar detta, och den visar också symbolen för translationsrelationen:

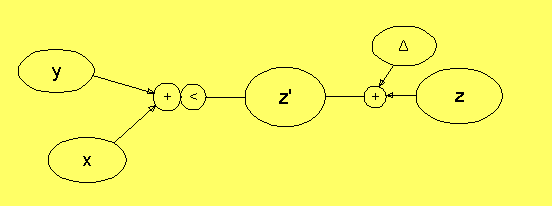
I följande exempelprogram visas mängden av translationer av en kub inuti i en pyramid. Tryck på return, så visas resultatet i gult. Tryck på return igen för att avsluta. Klicka sedan på "tillbaka" för att återvända.

Tidsuppdatering

Det finns inte någon, en gång för alla given, relation mellan ett nodvärde vid en tidpunkt, och samma nodvärde vid en annan tidpunkt. Ett dynamiskt system har dock en uppsättning variabler x_i (tillståndsvariabler), som kan ses som koordinater för en punkt (tillståndet) i ett tillståndsrum. Den utmärkande egenskaper för tillståndsvariablerna (och också för tillståndet) är att det finns en relation mellan dessa för en tidpunkt och för en annan. Den tar formen av en funktion Φ_t₁,t så att

x_i(t₁) = Φ_t₁,t( {x_i(t) })

System är vanligtvis tidsinvarianta så att Φ bara beror på t₁ - t och inte på t₁ och t var för sig. Om vi håller ihop alla tillståndsvariablerna i en n-dimensionell nod, x, så kan vi skapa ett nät, som beräknar tillståndet Δt tidsentheter längre fram.

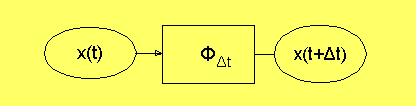
Detta är nu en modell av systemet. I det sammanhanget kräver man också att tillståndvariablerna (eller tillståndet) skall karakterisera systemet så väl, att varje storhet, y, som modellen är relevant för, skall kunna beräknas ur x som h(x). Vi kan nu tänka oss att Δt är given, och att aktuell tid är underförstådd i systemet, så att x(t) kan kallas x. x(t+Δt) kallar vi då för x⁺ (nästa tid). Då kan vi rita modellen som:

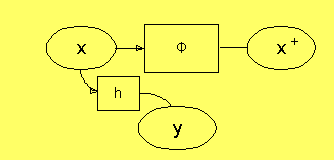
Nu kan vi göra ett tidsskift, och låta den underförstådda tiden gå från t till t+Δt. Därmed är det noden x⁺, som innehåller rätt värde på x, så vi bör flytta värdet i x⁺ till x. Nu har det ingen betydelse vad x var tidigare, så vi skall inte unifiera med x, utan vi har en process, där vi direkt skriver i noden utan unifiering. Vi markerar detta med en pil in i noden, vilket vi annars aldrig har. y har inte längre något samband med vad y var tidigare, utan y skall räknas ut ur x genom unifieringar. Därför måste vi vid tidsskiftet sätta y till u (unknown).

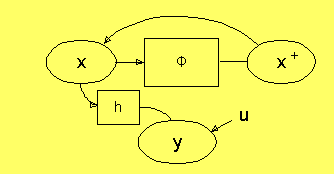
Ett annat synsätt på detta visas i följande figur. Där betyder P i x^P "previous" dvs. föregående värde. Tidsskiftet innebär att värdet i noden x "degraderas" till att representera föregående värde. Nuvarande värde kan vi nu skapa genom att unifiera genom funktionen Φ:

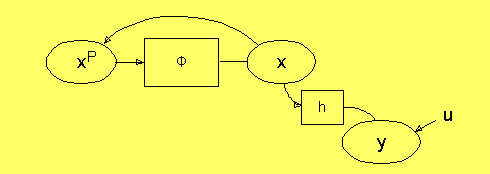
Noden y kan nu representera en storhet som vi kan mäta. Vi får in mätsignalen från omvärlden i en mätvärdesnod, men vi måste sedan uttrycka att mätapparaten kan mäta fel, genom att addera en osäkerhet till mätvärdet. Då får vi i noden y ett korrekt bud på storheten y. Vi kan också vara osäkra på om funktionen Φ verkligen ger oss en exakt prediktion av tillståndet, och vi kan uttrycka detta genom att addera en osäkerhet e_s någonstans. I figuren har vi ritat e_s som ett extra argument till Φ, som kan uttrycka externa men okända krafter etc.

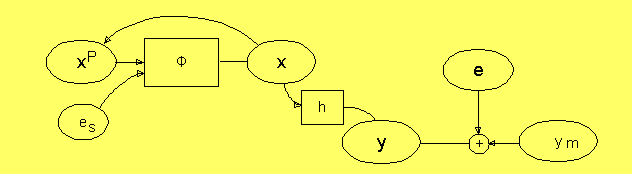
Nu kan vi iterera fram x över tiden, men vi kan också dra slutsatser om x genom att transportera mätvärdena i y baklänges genom h och unifiera. Detta ser ut som ett Kalmanfilter. Om funktionerna Φ och h är lineära, och alla variabler är stokastiska variabler med Gaussisk fördelning initialt, och om mätfelen och störningarna, som vi här tar hänsyn till genom tilläget av osäkerheterna e och e_s, är Gaussiska vita brus, så blir alla variabler Gaussiska även i fortsättningen, och därmed är alla förutsättningarna uppfyllda för att man skall kunna använda ett Kalmanfilter. Om vi i vårt relationsnätverk representerar osäkerhet med stokastiska variabler, så blir detta system identiskt med ett Kalmanfilter. Detta visas här [pdf]. Men relationsnätverket fungerar även med godtyckliga fördelningar och olineära funktioner.

I Kalmanfiltret är det nödvändigt att bruset, tex. e är vitt. Här fungerar detta så här: Om vi unifierar noden e, så kan vi faktiskt bestämma e med en osäkerhet, som bestäms av vad vi har för osäkerhet om x. Men till nästa mättillfälle har vi ingen nytta av detta, om vi vet att bruset är vitt. Då måste vi i samband med tidsskiftet ladda om noden e med ett mått p brusets styrka. (Vi skall egentligen ladda e med u, men sedan får vi ansluta e till en nod, som är skyddad vid tidsskiftet, och som innehåller ett intervall, som svarar mot brusets styrka.) Men om bruset inte är vitt, så kan vi utnyttja detta, så att vi laddar e med ett värde som baseras på e's tidigare värde, men som tillför en osäkerhet. Med andra ord tillför vi en dynamikmodell för e av samma slag som för x. På så sätt kan vi hantera icke- vitt brus. I Kalmanfiltret får man istället göra så kallad noise whitening.

Mängdrepresentation

Sedan man beslutat sig för att representera osäkerhet med mängder, så återstår att i sin tur representera mängderna med någon datastruktur. Därefter söker man för en mängdoperaton, t.ex. ∩, en motsvarande operation på datastrukturen, ∩_D, så att följande diagram kommuterar:

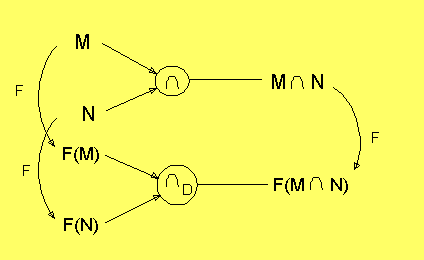
F är här den funktion, som för en given mängd ger motsvarande datastruktur. Man förväntar sig att F har en invers. I så fall har vi en isomorfism mellan mängdvärlden och datastrukturvärlden, och det är då också klart att varje operation i mängdvärlden har en motsvarighet i datastrukturvärlden. Svårigheten är bara att hitta den, och ingenjörsmässigt realisera den.

För att representera mängder, använder vi begreppet konvexa höljet. Om våra mängder är delmängder av ett vektorrum, så vet vi vad som menas med en rät linje. Speciellt vet vi vad som menas med en rät linje mellan två punkter P och Q. Vi identifierar punkter med ortsvektorer från ett givet origo till punkterna. Då är

L_PQ(α) = P + α(Q-P)

en punkt på den räta linjen mellan P och Q, om α tillhör intervallet I=(0,1). Hela linjen är då L_PQ(I). En mängd M är konvex om

L_PQ(I) ∈ M om P ∈ M och Q ∈ M

Det konvexa höljet C(M) till M är nu den minsta konvexa mängd, som innehåller M.

Nu kan vi representera konvexa mängder M, som har plana sidor, som

C(mängden av hörnpunkter i M)

Mängder som inte har plana sidor kan godtyckligt väl approximeras med sådana här mängder.

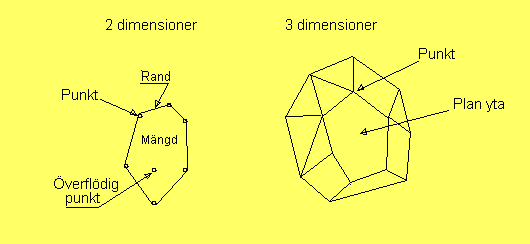
De plana sidorna blir månghörningar, som kan ha tre eller fler kanter. Om de har fler än tre kanter, dvs inte är trianglar, kan de i alla fall delas upp i trianglar. Då är hela randen till mängden beskriven som en union av trianglar. Därför kallas denna representation för en triangulering av mängden (eller dess rand). Begreppet går tillbaka till Henri Poincaré.

Språkligt utgår den här beskrivningen från en 3-dimensionell värld, men själva representationen fungerar i godtyckliga dimensioner.

Icke-konvexa mängder får representeras som unioner av konvexa mängder, kallade u-komponenter. Hela representationen av en mängd består då av en uppräkning av tal p[i][j][k], där index i pekar ut en u-komponent, index j pekar ut en punkt i representationen av den u-komponenten, och k pekar ut den k:te koordinaten för den punkten.

Många operationer är lätta att applicera på den här representationen. Lineära funktioner f, realiserar man genom att avbilda varje punkt i representationen genom f. Om man tillämpar samma princip för icke lineära funktioner, så får man ett fel. f(M) har då icke-plana sidor, men den representation man får fram av f(M), har med nödvändighet plana sidor. Om felet blir för stort får man först representera M med flera punkter, alltså flera trianglar. En välartad funktion avbildar tillräckligt små trianglar på en ytor som är tillräckligt nära plan.

Man kan också utnyttja att de flesta operationer är dilationer, dvs sådana att de kommuterar med union. Då kan man utföra operationerna på varje u-komponent för sig. Resultatet är sedan unionen av de avbildade u-komponenterna, och det är underförstått redan i representationen.

Emellertid är representationen av mängdskärning, ∩, en stötesten. För att realisera den går vi till en alternativ definition av konvexa höljet:

C(M) = skärningen av alla halvrymder som innehåller M

I tre dimensioner är en halvrymd det, som ligger på ena sidan av ett plan. Vi generaliserar ekvationen av ett plan till godtycklig dimension så här:

a₀ + a₁x₁+ + a₂x₂+ ... + a_nx_n = 0

Ekvationen för en halvrymd ges då av

a₀ + a₁x₁+ + a₂x₂+ ... + a_nx_n > 0

Om vi nu får "fel" sida av planet, så behöver vi bara byta tecken på alla a_i. Av "alla" de halvrymder, som ingår i definitionen, så är de flesta överflödiga, därför att de blir överspelade av andra halvrymder i skärningsprocessen. De som inte är överflödiga är de som tangerar de plana ytorna som avgränsar figuren. Det är lättast att utgå från trianglarna i trianguleringen, men om en del trianglar är delar av en större plan yta, så får vi ett antal identiska halvrymder, vilket kan ge vissa tekniska problem.

Nu består representationen av ett antal koeffecienter a[i][j][k], där index i pekar ut en u-komponent, där j pekar ut en viss halvrymd för den u-komponenten, och k pekar ut en viss koeefecient i ekvationen för den halvrymden.

Låt nu en u-komponent M_i av M vara given. För den har vi en lista av halvrymder. För en u-komponent N_j av N har vi också en lista av halvrymder. Om vi sammanför dessa listor till en, så har vi halvrymdsrepresentationen av skärningen M_i ∩ N_j. Sedan kan vi bara utnyttja att union distribueras över skärning.

(⋃M_i) ∩ (⋃N_j) = ⋃_ij (M_i ∩ N_j)

Vi behöver nu en funktion H som förvandlar en punktrepresentation till en halvrymdsrepresentation samt dess invers. Då har vi:

M_D ∩_D N_D = H^-1(H(M_D) ∩_H H(N_D))

Bildrepresentationen

En bild kan ses som en tunn mängd av intensiteter, som "svävar" över ett pixelplan. Om man för varje pixel lägger till en osäkerhet i intensitet, får man en mängd, som inte är tunn. I princip bör man lägga till så mycket osäkerhet till varje pixel, att intensiteten inte diskontinuerligt hoppar från en pixel till dess granne. Nu representerar en bild ett skal av intensiteter som svävar över pixelplanet. En sådan mängd kan naturligtvis representeras på det sätt vi beskrivit förut, men det blir en slösaktig representation, där vi måste ange 8 hörnpunkter för varje pixel, och vi utnyttjar inte att x- och y-koordinaterna är bestämda i ett fixt gitter. Det är bättre att representera en bild som två matriser bl_ij och bu_ij, som ger nedre och övre intensitet för den pixel som har plats (i,j) i pixelgittret. Representationen med övre och nedre gräns för intensitet representerar en inskränkning, eftersom vi inte kan representera unioner av icke disjunkta intervall. Med denna representation införd, kallar vi den tidigare för en koordinatrepresentation.

Vi kallar också mängder som ges i koordinatrepresentation för koordinatmängder och mängder som ges i bildrepresentation för bildmängder (Oegentligt eftersom de är mängder, rätt och slätt) och vi tala också om koordinatnoder och bildnoder. Nu måste vi införa transformationer mellan de båda representationerna, och vi måste införa operationer på bilddatastrukturen, som svarar mot olika mängdoperationer. Bildrepresentationen är sådan att den också kan hantera färgbilder. I princip har vi då en mängd som hör hemma i R⁵ med två pixelkoordinater och 3 koordinater för en RGB rymd. Tekniskt placerar vi i bl och bu data för de tre färgerna packade i 1 dataord. Det betyder att vi för varje pixel kan representera en parallellepiped i RGB-rymden. Den karakteriseras av de båda ändarna av sin huvuddiagonal, som finns packade i bl resp bu. Det här innebär ytterligare en inskränkning av vad vi kan representera i bildrepresentationen.

Språket Retina

Ett särskilt språk har utvecklats för att realisera relationsnätverksfilter. Det heter Retina efter Relation Network Analyser, eller efter ett latinskt ord ung. retina som betyder nät. Numera skrivs det med XML-notation. Syntaxen beskrivs här med tecknen < och > utbytta mot [ och ] för att inte aktivera webbläsarens känslor för HTML-språket.

retina-program = [net] body [/net]
body = noder relationer instruktioner
noder = [nodes] konstanter och variabler [/nodes]
konstant = [const] nodbody [/const]
variabel = [var] nodbody [/var]
nodbody = [id] namn [/id][dim] n [/dim][value]xxx[/value] eller

nodbody = [image][id]namn[/id][slot]i[/slot][/image]
relationer = [relations]relation relation ... [/relations]
relation = [r][e] ekvation [/e][id] identitet [/id][/r]
ekvation = [RTYP][n]nod1[/n]...[n]nodn[/n][/RTYP]
instruktioner = [i]instruktion[/i]
instruktion = [ITYP] argument [/ITYP]

Mellan parenteserna [nodes] och [/nodes] står det alltså ett godtyckligt antal konstanter och variabler, gärna blandade i ordning. Strängen xxx är en värdeangivelse för att ange begynnelsevärde i noden i en speciell syntax. Denna value-del är valfri, och om inget värde anges, så tilldelas noden en representation för u="okänt" (unknown). Om man önskar en oövrskrivbar nod med värdet u, så kan det alltså vara relevant att införa en konstant utan att tilldela den något värde. Parentersrna [dim][/dim] innesluter variabelns dimension, dvs dimensionen på det vektorrum, där den är inbäddad. Om en nod rymmer en bildnod inkapslas den i en parentes med taggen 'image'. Bilderna placeras på fasta positioner (slots) i systemet, och vilken slot en viss bild hamnar i anges mellan parenteser med samma slots. Man kan lägga olika bilder på samma slot om man inte behöver dem samtidigt.

För relationerna finns en given uppsättning typer, som symboliseras med taggen RTYP. För relationerna anges de noder, som är anslutna till relationen, och hur många de är bestäms av relationen. Vissa relationer kan ha ett variabelt antal noder. Se mera här.

Instruktionerna styr hur transporter och unifieringar görs i nätet, men också hur resultat listas eller visas grafiskt. Det finns en given uppsättning instruktioner, som symboliseras med taggen ITYP. Olika instruktioner har olika slags argument, som innesluts med olika XML-parenteser med olika taggar. Se mera här.

Relationer i Retina

Följande relationer finns implementerade för koordinatnoder Beträffande bildnoder se här. Observera också att det inte finns någon graf-relation. Praktiskt har genereringen av en graf utförts som en grafinstruktion

EQUALS. Har två noder. Transporten innebär att budet på den ena noden = värdet på den andra. Efter ömsesidig unifiering kommer båda noderna att innehålla skärningen av de tidigare värdena i noderna.
SUBSET. Har två noder. Relationen uttrycker att nod 1 ⊆ nod2. Budet på nod1 = värdet av nod2. Budet på nod2 är okänt (En delmängd säger ingenting om den mängd den är en delmängd av). Tekniskt kan man använda detta för att skydda nod2 mot nod1.
CART, Cartesisk produkt. Har N noder. nod1 = nod2 × nod3 ... × nodN. Budet på nod1 är den Cartesiska produkten av de övriga. Vid transport till övriga noder är budet en projektion av rätt komponent av nod 1 utan hänsyn till vad de övriga noderna innehåller. (se ovan)
UNION. Har N noder. nod1 är unionen av de övriga. Vid transport till nod1 är budet unionen av de övriga. Vid transport till övriga noder är budet = värdet av nod1. Detta är det minst djärva antagandet. Om övriga noder innehåler något område, så maskerar de möjligheten att veta om den aktuella noden innehåller samma område.
HULL, konvexa höljet. Har N noder. nod1 är konvexa höljet till unionen av de övriga nodernas värden. Detta är budet på nod1. Transport till övriga noder har ingen effekt.
SECTION, mängdskärning. Har N noder.Denna relation är egentligen obehövlig genom att man kan använda EQUALS eller SUBSET tillsammans med unifiering, som ger mängdskärning. Men relationen finns och innebär att nod1 är skärningen av de övriga. Transport till övriga noder har ingen effekt.
ALT, alternativrelation. Har N noder. nod1 = någon av de övriga, nämligen den första av dem, som går att unifiera med nod 1 utan att resultatet blir den tomma mängden. Budet på övriga noder = värdet av nod 1.
SUM, summa. Har N noder. nod1 är summan av de övriga. Budet på någon annan nod = nod1 minus summan av de övriga.
TRANSL, translationsrelationen beskriven ovan. Har 3 noder. Budet på nod3 = mängden av alla translationer av nod2 så att den ryms i nod1, alltså så att nod2 + nod3 ⊆ nod1. Relationen är symmetrisk mellan nod2 och nod3. Budet på nod1 = summan av nod1 och nod2
MULT, matrismultiplikation. Har 3 noder. nod1 och nod3 har dimensionen N och betraktas som vektorer. nod2 innehåller en union av N vektorer, och betraktas som matrisen med dessa vektorer som kolonnvektorer. Budet på nod1 = nod2·nod3. Budet på nod3 = nod2^-1 ·nod1. Transport till nod2 har ingen effekt.
SCALAR, multiplikation med skalär. Har 3 noder. nod1 och nod3 betraktas som vektorer av samma dimension. nod2 skall innehålla en variabel av dimension 1 (en skalär). Budet på nod1 = nod2·nod3. Budet på nod3 = nod2^-1·nod1. Transport till nod2 har ingen effekt.
SQR, kvadrat. Har 2 noder, båda av dimension 1. nod1 = nod2². nod2 är kvadratens invers ur nod1. Den avbildar mängden av en punkt på mängden av punktens kvadratrot och -punktens kvadratrot. Intervall av bildas på intervall. Om nod1 är ett negativt intervall så blir budet på nod2 den tomma mängden
BOX. Har 2 noder. Budet på nod1 är en omskrivande rektangel (parallellepiped etc.) runt nod2. Transport till nod2 har ingen effekt.
PYTH, relationen z² = x² + z². Relationen skulle kunna byggas upp av SQR och SUM och fungerar på samma sätt.
POLY, polynom. I en inkarnation har relationen 3 noder. nod2 är k-dimensionell och innehåller de k koeffecienterna i ett k:e-gradspolynom av x. Det är meningen att mängden här skall vara en punkt i R^k (ingen osäkerhet). Nod 3 innehåller en endimensionell variabel x, som däremot kan ha formen av intervall eller unionen av intervall. nod1 ger bilden av x under polynomet. I en andra inkarnation har relationen 2 noder. nod 1 innehåller grafen för ett polynom. Budet på nod2 är en skattning av de k koeffecienterna i det polynom som har grafen i nod1. Lagranges interpolationspolynom används.
GAUSS, en gaussfunktion. Har samma inkarnationer som föregående. I den första är nod 1 värdet av Gaussfunktionen för det x som finns i nod 3. Parametervärdena medelvärde och varians finns i nod 2. I den andra inkarnationen skattas medelvärde och varians till nod 2 från en graf i nod 1.
POLAR, omvandling till polära koordinater. I nod1 finns en mängd i 3 dimensioner. Vid transport till nod2 är budet mängden av (avstånd, bäring, elevation)-triplar för punkterna i nod1. Budet på nod1 är mängden av punkter, som har (avstånd, bäring, elevation)-triplar som finns i nod2.
GROUND, projektion till ett markplan från en projektor på höjden h. I nod1 finns bilden i projektorn uttryckt som vinklar, alltså bäring och elevation. Höjden h finns som en tredje koordinat i både nod1 och nod2. Därutöver är budet på nod2 projektionen av bilden på ett markplan på höjden 0. Budet på nod1 simulerar en kamera, som fotograferar bilden på marken.
ROTATED, en rotation i planet. Har 3 noder. nod2 innehåller en plan figur, och nod3 en vinkel. Budet på nod1 är figuren roterad med vinkeln. Budet på nod2 är figuren i nod1 roterad i motsatt rikning. Transport till nod 3 har ingen effekt.
TWISTED, en vridning. Har 2 noder. nod2 innehåller en tredimensionell figur. Den tredje dimensionen skall betraktas som en vinkel. Budet på nod1 är en vriden figur, där varje punkt är vriden runt z-axeln med den vinkel som gäller på punktens höjd.
EULER, tranformationsmatris. Har 2 noder. nod2 är tredimensionell och betraktas som tre Eulervinklar (gir, tipp och roll). Budet på nod1 är motsvarande transformationsmatris representerad som unionen av sina kolonnvektorer.
PROJECTED, en projektion på ett godtyckligt lutande plan. nod2 innehåller en godtycklig tredimensionell figur F. nod3 representerar ett plan i form av en triangel i R³ med sina tre punkter i planet. Budet på nod1 är F projicerad på planet, alltså en 2-dimensionell figur. Origo i planet ligger i den representerade triangelns första punkt.
AVERAGE, medelpunkt. Har 2 noder. Budet på nod1 är en medelpunkt i den mängd som finns i nod 2. Medelpunkten beräknas som tyngdpunkten av alla punkterna i representationen av mängden, där alla punkterna har massan 1
UPPER, övre extrempunkt. Budet på nod1 är en extrempunkt för mängden i nod 2. Det är den punkt i den omskrivande parallellepipeden, som har störst värden på alla koordinater
LOWER, nedre extrempunkt. Budet på nod1 är en extrempunkt för mängden i nod 2. Det är den punkt i den omskrivande parallellepipeden, som har minst värden på alla koordinater
DNEWTON, en farkost som i enlighet med Newtons kraftekvation har en begränsad acceleration. Den kan arbeta dels med dimensionen 4 för en farkost som kan röra sig i planet, och dels med dimensionen 2 för en farkost som kan röra sig längs en väg. Det finns ytterligare relationer till noder som innehåller ett vägsystem, som kan förgrena sig. nod2 innehåller mängden av tänkbara positioner och hastigheter för farkosten. Budet på nod1 blir en prediktion av denna mängd framåt i tiden. Prediktionstiden anges i nod4. Accelerationsförmågan anges i nod3.
NEWTON. Relationen DNEWTON ger en mängd i nod1, som måste representeras av fler punkter än mängden i nod2. Om man itererar ett system genom att återcirkulera värdet i nod1 till nod2, får man en mer och mer komplex mängd. Relationen NEWTON löser detta genom att representera mängden med en approximation med ett fixt antal punkter.I vägfallet är det 4 punkter. I fallet med rörelse i planet sker en projektion, som eliminerar korrelationer mellan x- och y-riktningarna. Representationen kan då göras med 8 punkter. nod 2 måste innehålla en mängd i positions-hastighets-rymden som har standardformen med ett fixt antal punkter. För att konvertera godtyckliga mängder i en positions-hastighets-rymd till standardformen finns en relation NEWTONAPPROX.

Bildrelationer

Många av relationerna har en tolkning i termer av mängder, som egentligen inte skall påverkas av om mängderna är representerade på koordinatform eller bildform. Vissa relationer kan användas för konverteringar mellan de båda formerna. Vi kan ta Cartesisk produkt som ett exempel:

Bild = Pixelplan × Intensitet

I noden bild har vi en bildmängd. Om denna bildmängd har pixlar med tomma intensitetsmängder, så får vi i noden Pixelplan en binär bild, som är 0 där vi hade tom intensitet och 1 annars. De binära värdena 0 och 1 representeras på ett speciellt sätt, så att 0:orna kan tolkas som tomma intensiteter, och så att en visualisering av bilden kan göras. 1:orna representeras som vit färg. Men vi kan också ta ut resultatet som en koordinatmängd, genom att deklarera Pixelplan som en koordinatnod. Här får vi då ut mängden av pixelkoordinater, där Bild har en icke-tom intensitet. Det här blir normalt sätt en mängd med en komplicerad representation, så det är nödvändigt för systemet att på något sätt föra samman sammanhängande områden med 1:or. Givet en bild i noden Bild, kan vi också projicera ut dess intensitetsrepertoar eller färgrepertoar genom noden Intensitet. Men vi kan också skapa bilder genom att förse noden Pixelplan med en plan figur och noden Intensitet med en färg. Bild blir en bild med en enfärgad figur med tomma intensiteter därutanför, men vi kan bilda flera sådana bilder och ta unionen mellan dem.

Summarelationen är ytterligare ett exempel:

Bild = Bild1 + xyz

Om vi har koordinatrepresentationen för en punkt i xyz så får vi i noden Bild en förskjuten kopia av Bild1. Det följer av defintionen av summa. Vi kan förskjuta bilden även i intensitetsled genom att ha z-koordinaten i xyz skild från 0. Om vi låter xyz vara en 5 dimensionell mängd, så tolkas de tre sista koordinaterna som färgdkoordinater, och då kan vi förskjuta bilden i färg. Om xyz är en utbredd mängd, så blir Bild en suddig kopia av Bild1.

Om xyz också är en bild, så finns det en ortodox tolkning av hur Bild, skall beräknas utifrån definitionen av en summa av mängder

X + Y = { x + y | x ∈ X, y ∈ Y }

Den tolkningen, när X och Y är bildmängder kräver emellertid en enorm mängd beräkningar, och resultatet är också komplicerat och svårtolkat. Å andra sidan finns det ett behov av att lägga ihop 2 bilder pixel för pixel, och det är för denna tolkning som relationen används i Retina-systemet. I varje pixel görs additionen av intervall enligt definitionen av summa ovan.

Translationsrelationen skulle fungera också för bildmängder, och har en viktig uppgift för att leta efter mönster i bilder. På grund av tillämpningarna har dock delmängdsrelationen vänts från ⊆ till ⊇, så att relationen skrivs

Bild ⊆ S + xyz

Bild är här en bildnod. S är en koordinatmängd, som fungerar som en slags specifikation för vad vi letar efter i bilden. Budet på nod xyz är mängden av translationer (både i pixelled och intensitetsle) som är sådan att S innehåller Bild. Oftast är S en liten figur, som upptar en mindre del av bildytan. För att det skall fungera måste då S kompletteras utanför figuren med stora intensitetsintervall.

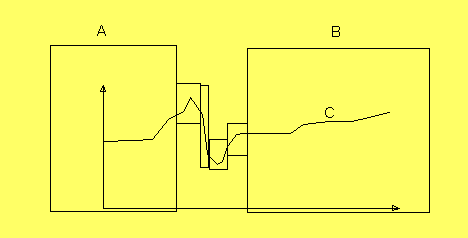
I figuren, som visar en en-dimensionell bild, är C bilden i nod Bild. A och B är utfyllnaderna med stora intensiteter utanför den sökta figuren. Den egentliga sökta figuren är rektanglarna mellan A och B.

För bilder är den kompletta processen med transport till ett bud och sedan unifiering mindre intressant. Rent praktiskt använder man bara transportprocessen och den innebär att det beräknade budet skrivs över det som fanns tidigare i noden. Det är också ovanligare i bildfallet att man använder relationer i båda riktningarna. Användningen av relationsnäten påminner då mera om traditionell signalbehandling genom "svarta lådor", och detta påverkar också sättet att beskriva relationerna i det följande.

EQUALS. Om båda noderna är bildnoder, så kopieras bilden från den ena noden till den andra. Om en nod är en koordinatmängd, så genererar den en syntetisk bild som läggs i bildnoden. Transport till koordinatnoden har ingen effekt.
CART, cartesisk produkt (×) har beskrivits ovan
UNION. Den korrekta tolkningen av union mellen bilder faller ut som union pixel för pixel. Inskränkningen som är inbyggd i representationen av intensitet i varje pixel med en övre och nedre gräns spelar emellertid roll här. Om resultatet av unionen blir en mängd av icke disjunkta intervall, måste de ersättas av ett intervall, som täcker alla. Transport till andra noder än nod 1 har ingen effekt
SECTION. Mängdskärning realiseras korrekt som mängdskärning pixel för pixel.Transport till andra noder än nod 1 har ingen effekt
ALT. Har 3 noder som alla är bildnoder. Bild1 blir identisk med Bild 2 i alla pixels utom där Bild2 har tom intensitet. Där hämtas pixlarna i stället från Bild 3. Transport till andra noder än nod 1 har ingen effekt
SUM, summa, har beskrivits ovan
TRANSL, translation har beskrivits ovan
MULT fungerar som för koordinatmängder, dvs nod2 innehåller en matris. Här måste emellertid matrisen vara en diagonalmatris (dvs systemet bortser från icke-diagonalelementen). Processen innebär att bilden skalas upp och ner i pixelled eller intensitetsled. Både nod1 och nod3 kan uppdateras, och vid uppdatering av nod3 används matrisens invers.
BLUEPRINT. nod1 blir en "blå" variant av nod2. Först beräknas ljusstyrkan i en pixel, och sedan representeras denna som ett tal mellan 0 och 255. Om bilden nu visas som färgbild blir den blå. Vid transport tillbaka till nod 2 kan man inte återställa färgen, men man får en gråskalebild i stället fär en blåskalebild
COMPLEMENT. Endera noden innehåller här en binär bild (med 0 representerat som ett tomt intervall, och 1 representerat som vitt) och i den andra noden genereras det logiska komplementet
NOTOVEFULL. Nod 2 skall här innehålla en binär bild. Om den inte har alltför många 1:or (gränsen anges i nod 3) så kopieras den till nod 1. Annars skickas en bild med enbart 0:or till nod 1. Denna beräkning är till för att bespara vissa andra beräkningar risken för överansträngning.
AVERAGE, UPPER och LOWER arbetar pixel för pixel, och har för varje pixel samma funktion som för koordinatmängder
OCCUR. Här räknar man hur många pixlar, som faller i en given pixellåda, som har en utsträckning i pixelled och intensitets/färgled. Sedan flyttas lådan omkring över pixelplanet, och för varje läge blir antalet ett intensitetsvärde i en resultatbild. Lådan läggs i nod 1, och behöver inte vara en enkel låda, utan kan vara en union av lådor. Om noden innehåller u-komponenter, som är mera allmänna mängder, så ersätts de emellertid av omskrivande lådor. nod2 innehåller den analyserande bilden. nod3 är frivillig men kan innehålla det område som skall avsökas. nod1 kommer att innehålla resultatet. Man kan bygga upp specifikationer av samma slag som i translationsrelationen, och operationen har ungefär samma funktion som translationsrelationen, men den har en viss immunitet mot brus i bilden, medan brus kan slå ut translationsoperationen helt och hållet. OCCUR-relationen genererar en bild och för att få ut positionen för funna objekt, måste man leta efter maxima i bilden.
OCCURCONTRAST. Ungefär samma som OCCUR, men här letar man efter kontraster i bilden i en given låda. Lådan är här ett tvådimensionellt objekt som bara avgränsar ett område i pixelplanet.
THINNED. nod2 innehåller en binär bild, och nod2 kommer att innehålla en mera uttunnad binär bild, där det vita området krymps ihop utan att bilden ändras topologiskt. Processen kan upprepas flera gånger.
DRAWN. nod2 innehåller en 2-dimensionell koordinatmängd och nod3 en bakgrundsbild. Budet på nod1 är bakgrundsbilden med konturen till mängden inritad. Används för resultatpresentation.
OCCLUDED. Uttrycker en relation mellan 3 bilder. bild2 innehåller ett föremål, som skymmer bakgrunden i bild3, så att den inte syns i bild1. Givet två av bilderna kan man säga något om den tredje. bild2 kan man få fram genom att se var bild1 och bild3 skiljer sig, och extrahera pixlarna ur bild1. Bild 3 kan man få ur bild1 utom på de ställen där bild1 och bild2 överensstämmer. Där är bild2 okänd.
CLUSTERS identifierar kluster, dvs sammanhängande områden med 1:or i en binär bild i nod2. Att klusterna är sammanhängande definieras av en en minsta bredd på "0:gator" som skall finnas mellan två områden, för att de skall betraktas som skilda kluster. Denna minsta bredd finns i nod2. I nod3 finns ett storleksintervall på kluster i antal pixels. Man kommer inte att registrera kluster som ligger utanför detta intervall i storlek. Resultatet i nod1 är en koordinatmängd med mittpunkter för funna kluster. Resultatet kan också presenteras i en bild, som visar olika kluster i olika gråskalor.
SAMPLED samplar ut punkter ur en bild till en koordinatmängd i nod1. Bilden finns i nod2. I nod3 finns det område som skall samplas ut och i nod4 finns en tvådimensionell punktmängd som representerar antalet punkter som skall samplas ut. Av de utsamplade punkterna kan man generera en specifikation till TRANSL-relationen eller boxar till OCCURS-relationen, och sedan kan man applicera dessa relationer på en annan bild och därmed få en korrelation mellan bilderna.
SAMPLEDNONFLAT samplar också ut punkter ur en bild men bara på ställen där det finns kontraster i bilden. Bilden avsökes här slumpmässigt inom ett givet område tills tillräckligt många samples har hittats. Den samplade bilden finns i nod2. Det avsökta området finns i nod3 och det önskade antalet samples finns i nod4.

Instruktioner i Retina

Följande instruktioner finns i Retina. I syntaxen ersätter de parenteserna med taggen ITYP med innehåll. Här anges instruktionernas namn och taggarna på de XML-parenteserna som innehåller argumenten.

UNIFY thru to m . Detta är den grundläggande operationen i ett relationsnätverk. Ett bud beräknas för noden to beräknat på dess grannar runt relationen thru. Detta unifieras sedan med vad som redan står i noden. Unifiering görs som mängdskärning, som är en relativt komplicerad operation, och det kan vara ibland vara nödvändigt att arbeta med förenklade varianter, som t.ex. kan utnyttja att data kan ha en viss speciell struktur. Sådana varianter kan man ange med hjälp av argumentet m.
TRANSPORT thru to Detta är en enklare variant där man placerar det bud man räknat ut direkt i noden, utan hänsyn till vad som stod där förut. Detta kan användas då man vet att noden dessförinnan innehåller värdet u. Det kan också användas då man transporterar information genom en kedja av relationer. Man behöver då bara göra unifieringen på ett ställe längs kedjan och kan sedan transportera resultatet till andra noder. Då to-noden är en bildnod, är det också bara transport, som kommer ifråga. Argumenten är de samma som för unify, utom att m saknas.

GRAPH to x y chain. Detta är den instruktion som i praktiken realiserar idén om en grafrelation. Den färdiga grafen placeras i noden to. Relationen är en relation mellan noderna x och y. Men själva relationen konstitueras genom argumentet chain. Innehållet mellan XML-parenteserna taggade med chain heter kanske 'c'. Då skall det finnas instruktioner som är märkta med taggen 'c' i stället för med taggen 'i'. Dessa instruktioner exekveras som ett led i grafberäkningen, men ignoreras vid den vanliga exekveringen av instruktionen. Före exekveringen skall noden x förses med en lista av delmängder. Systemet laddar en delmängd i taget i noden x och exekverar sedan instruktionerna märkta med 'c'. Detta genererar ett värde på y och x × y blir sedan ett delbidrag till grafen. Unionen av dessa delbidrag laddas slutligen i noden to.
ASSIGN to from. Värdet i noden from läggs i noden to oavsett vad som fanns där förut.
WRITE node. Innehållet i noden node skrivs ut på "konsolen" i ett standardiserat format
ERASE color öppnar ett grafiskt fönster, om det inte redan finns, och fyller sedan fönstret med färgen color.
SCALE node sätter skalningen på grafiken, så att värdet i noden node fyller ut skärmen.
DRAW node color Värdet i noden node visas grafisk på skärmen i färgen color. Om det är tredimensionellt så ritas det i perspektiv, och i så fall skall skalningen enligt föregående instruktion ha givits av ett tredimensionellt objekt
REDRAW ritar om bilden
SHOW image visar bilden image på skärmen.
WAIT väntar på att operatören skall trycka på return-knappen.
LOAD to file hämtar en bild från filen file och placerar den i noden to.
LABEL label (label har här ingen egen XML-parentes utan den står direkt i instruktionens egna XML-parentes. Detta är en startpunkt för exekveringen, som man kan referera till utifrån.
RETURN innebär att exekveringen återgår till huvudprogrammet.

Exekvering av Retina

Retina programmet XMLRNF är en Java-klass (men vid demonstrationerna här en Java-Applet), som har en egen "main"-rutin för exekvering. Om man anropar den skall man ange en fil med Retina-kod (i XML-form) som argument. Men man kan också kapsla in XMLRNF-klassen i vilket programsystem, som helst, och i så fall lämna "main"-rutinen oanropad. Då skapar men en instans av klassen med en konstruktor, som tar en retina-fil som argument. Man kan obehindrat skapa många relationsnätverk med olika retina-filer i samma system. Retina-filerna kan tilldela värden till noder, men det finns också metoder i klassen för att ladda noder med:

put(PSet S, String name) laddar en given mängd av typen PSet till en nod med namnet name. Pset är den mängdrepresentation som används i systemet, och det kräver ett visst arbete för att sätta upp en sådan struktur.
put(double x, String name) laddar ett punktvärde till en en-dimensionell nod name
putImage(String name, Foto foto) laddar en bild i form av en instans av klassen Foto till noden name. Foto innehåller ett Java image-objekt, men också en uppackning av bilden till en array av pixlar, vilket Retina-systemet utnyttjar.

Sedan exekverar man relationsnätverket med

exec(String label) där strängen label skall finnas som en label i Retina-koden.

Därefter kan man hämta ut data ur nätet med getrutiner:

Pset get(String node)
void getImage(String node, Foto foto), som lägger bilden i nod node i ett befintligt Foto-objekt

Nu kan man iterera nätet igen, efter att ha laddat nya indata. De noddata, som man inte laddar om, har kvar sina värden.