Kaosteori

En kaotisk orbit

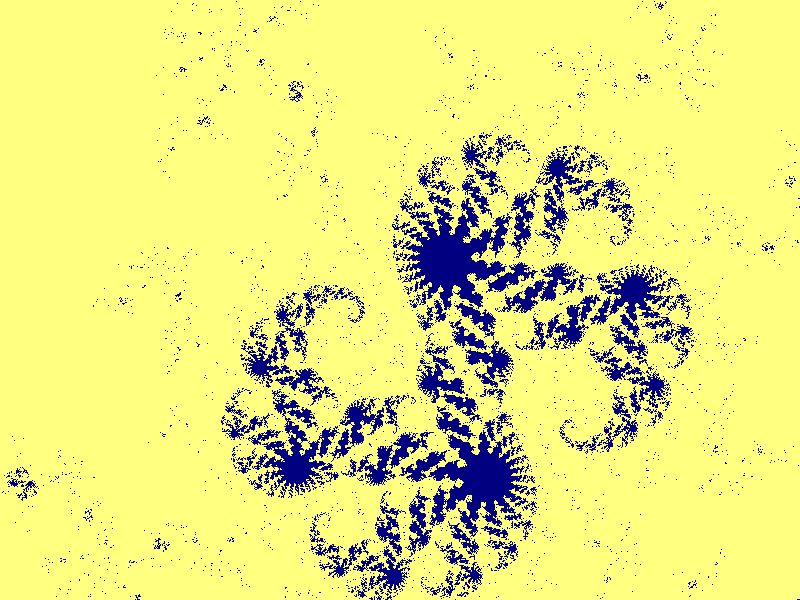
En kaotisk orbit till ett dynamiskt system är en orbit som rör sig inom ett begränsat område av tillståndsrummet, som inte konvergerar mote en punkt, och som inte återvänder till en punkt där den varit förut. En kaotisk orbit representerar alltså en aperiodisk rörelse. Därutöver finns krav, som utesluter alltför välordnade orbits från att kallas kaotiska. Ett system av två oscillatorer med ett irrationellt förhållande mellan frekvenserna, kan koordinatiseras som en torus, och varje orbit lindar sig kring torusen utan att någonsin stöta på sig själv. En sådan orbit är emellertid för välordnad för att få kallas kaotisk.

Feigenbaumbifurkation

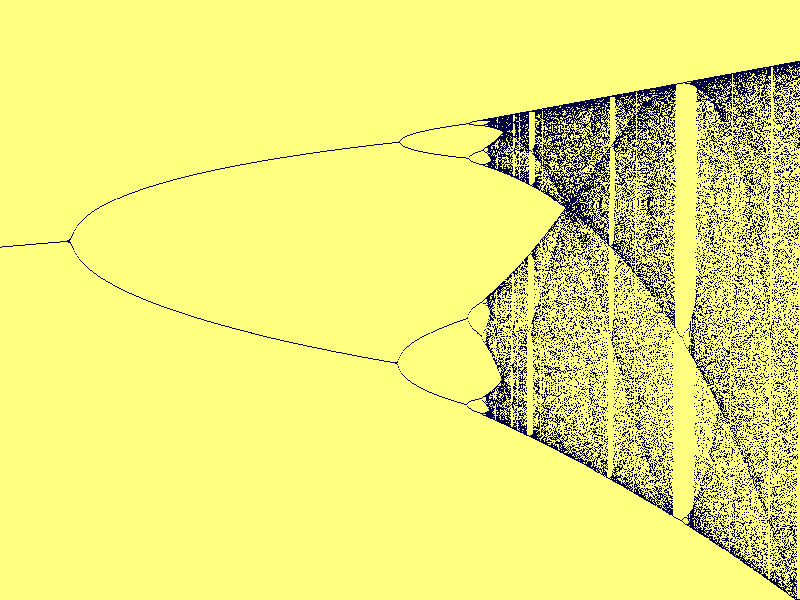
Intervallet 2.9 till 4 för alfa:



Juliamängden

Vi utgår från följande ekvation i det komplexa:

zn+1=zn2 + c
och bestämmer oss för ett värde på c. Vi startar ekvationen från ett värde z0. Frågan är då: från vilka z0-värden konvergerar systemet, och från vilka divergerar det. Man kan visa att om zn har beloppet större än 2, så divergerar systemet. Man får ett område med konvergens. För fallet divergens inför man det underliga språkbruket att man har konvergens mot oändlighetspunkten. På randen har man varken konvergens mot små värden eller konvergens mot oändlighetspunkten. För nästan alla punkterna har man heller inte någon n-periodisk gränscykel. Julia och Fatou införde då en mängd av punkter där man varken hade konvergens eller en gränscykel, och den mängden har kommit att få Gaston Julia's namn. Vad man hade på denna mängd var kaos, men den termen var okänd på Julia's och Fatou's tid på 1920-talet. Vi ritar några exempel på konvergensområden, och påminner om att randen på denna mängd är Julia-mängden. Det är lätta att visa att för c=0 är Julia-mängden lika med enhetscirkeln:



Om man nu ändrar c en smula, till 0.1+0.1i, så skulle man kunna tänka sig att cirkeln förskjöts en smula, och kanske blev elliptisk. Men den deformeras på ett ganska märkligt sätt:



Ännu mera händer: Här är Julia-mängderna för c=0.35+0.35i och c=0.7+0.37i:





Den här figuren, som äger rum vi c=-0.75 brukar kallas San-Marco-katedralen:



Den här figuren kallas "den svultna draken" och har sin plats vid c=-i. Den är egentligen helt fragmenterad, och består alltså av enstaka singulära punkter. Vi skulle egentligen inte ha en chans att stöta på dem. Vi har fått fram dem genom att bara iterera ekvationen 15 gånger. Om vi inte har fått divergens innan dess så godkänner vi punkten:

Mandelbrotmängden

Mandelbrotmängden runt punkten (0,0) med bredden 3:



Mandelbrotmängden runt punkten (-0.105, 0.804) med bredden 0.5:



Mandelbrotmängden runt punkten (-0.105, 0.924) med bredden 0.01



Mandelbrotmängden runt punkten (-1.25, 0.02) med bredden 0.05



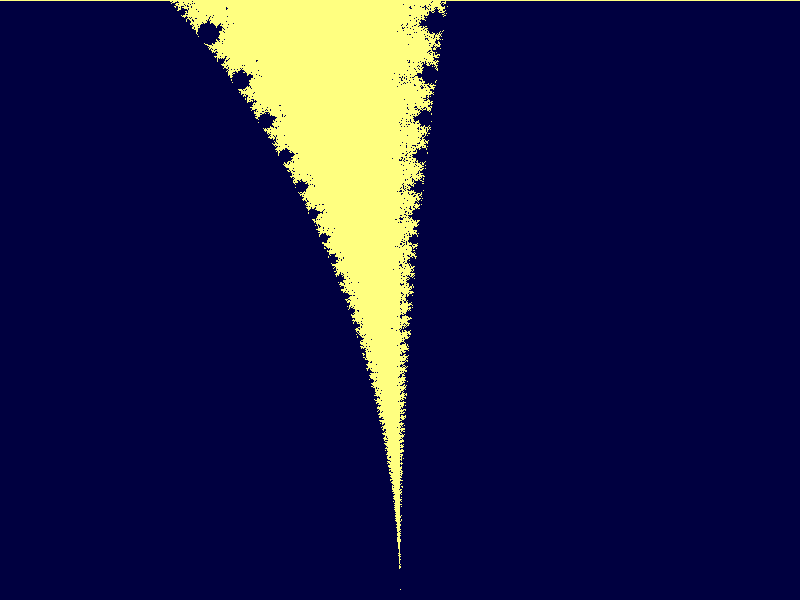
Mandelbrotmängden runt punkten (0.321006, -0.047637) med bredden 0.000819255:



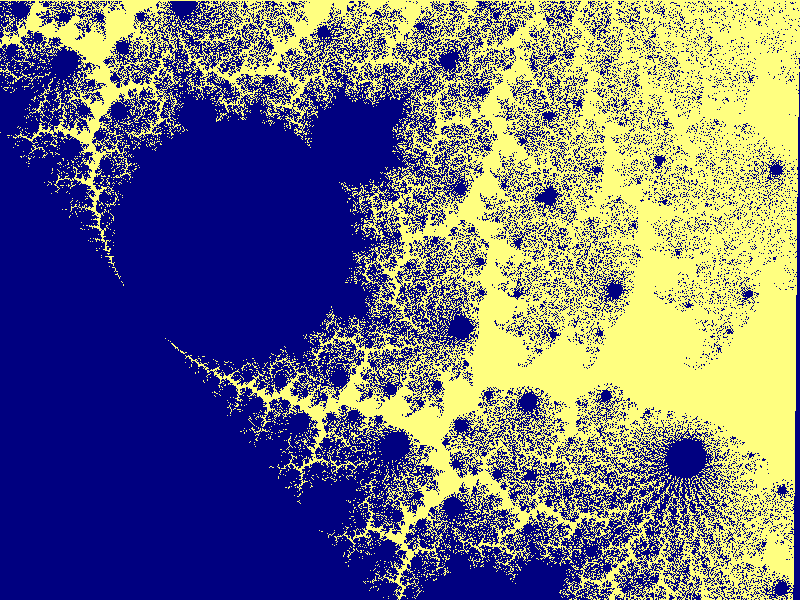
Mandelbrotmängden runt punkten (-1.24885, 0.01244043) med bredden 0.000833945:



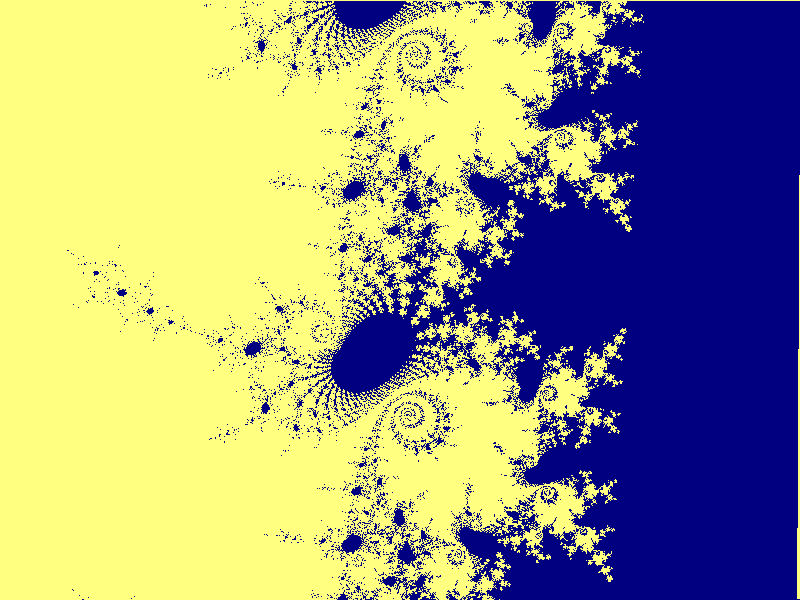
Mandelbrotmängden runt punkten (0.33348368, 0.064884255) med bredden 0.000033:



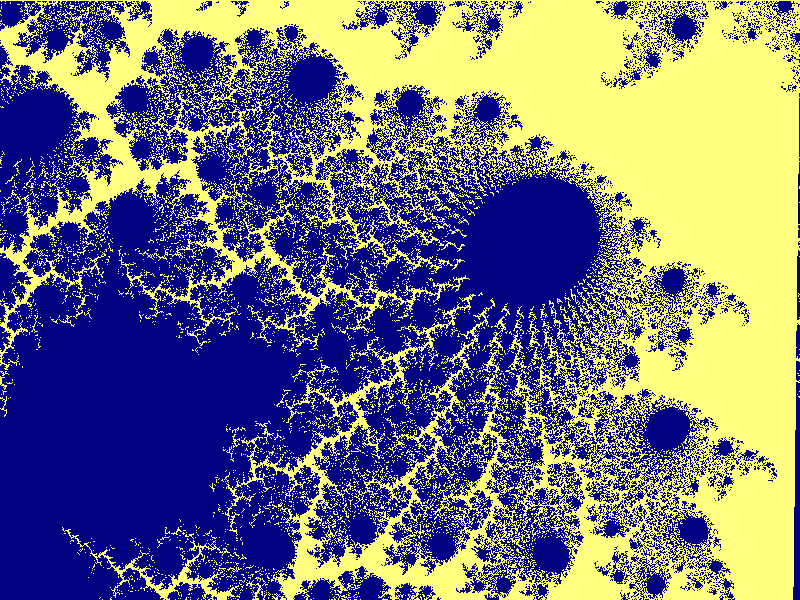
Mandelbrotmängden runt punkten (0.2830002573, -0.012592991 med bredden 1.59E-09:



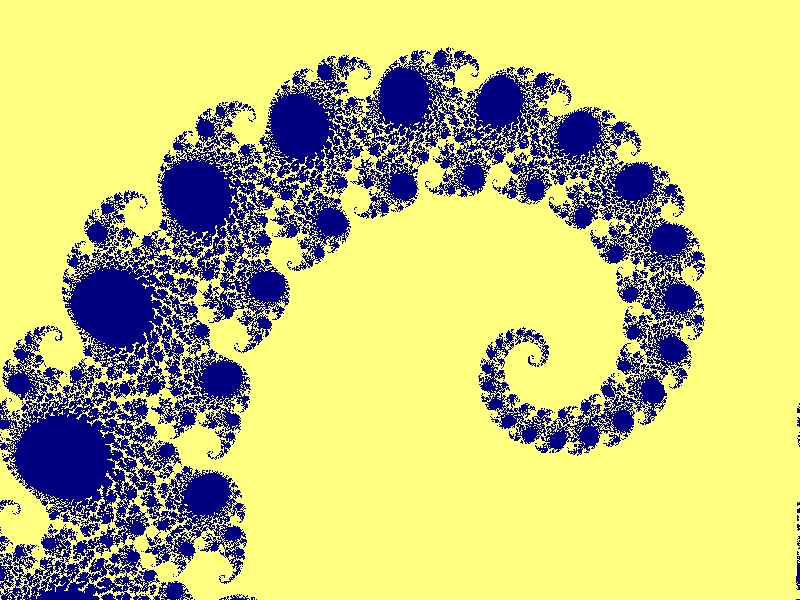
Mandelbrotmängden runt punkten (0.35667966,0.069754999999) med bredden 7.182E-5:

statyer Mandelbrotmängden runt punkten (0.27264547884375,0.0069791756) med bredden 1.42E-5: (Aku-Aku statyerna)

Mandelbrotmängden runt punkten (0.3309417,0.060585526) med bredden 1.0147E-4

Mandelbrotmängden runt punkten (-0.99829,0.287248) med bredden 3.157E-4

Mandelbrotmängden runt punkten (-0.9964612,0.28906234) med bredden 9.39E-6 (Blad)

Mandelbrotmängden runt punkten (-1.20593910,0.1628686) med bredden 6.679E-4

Mandelbrotmängden runt punkten (-1.16777768109259,0.245813283118458) med bredden 3.4848E-11

Mandelbrotmängden runt punkten (-0.234422546,0.827625200) med bredden 1.63E-6

Mandelbrotmängden runt punkten (0.305587404,0.0229187703) med bredden 1.12E-8

Mandelbrotmängden runt punkten (-0.917116825,0.27691706876) med bredden 3.85E-5

Mandelbrotmängden runt punkten (-1.476491685,-0.00501757796) med bredden 4.4535E-8

Mandelbrotmängden runt okänd punkt (Hamnen)

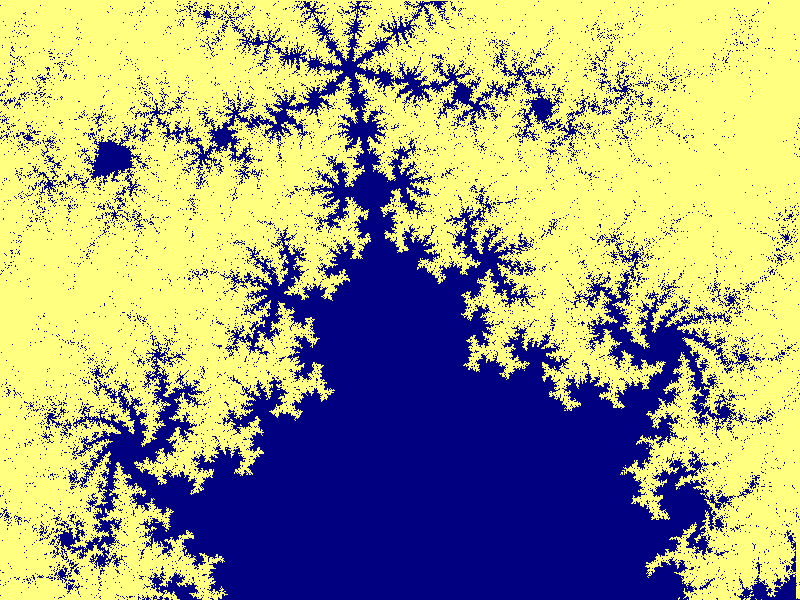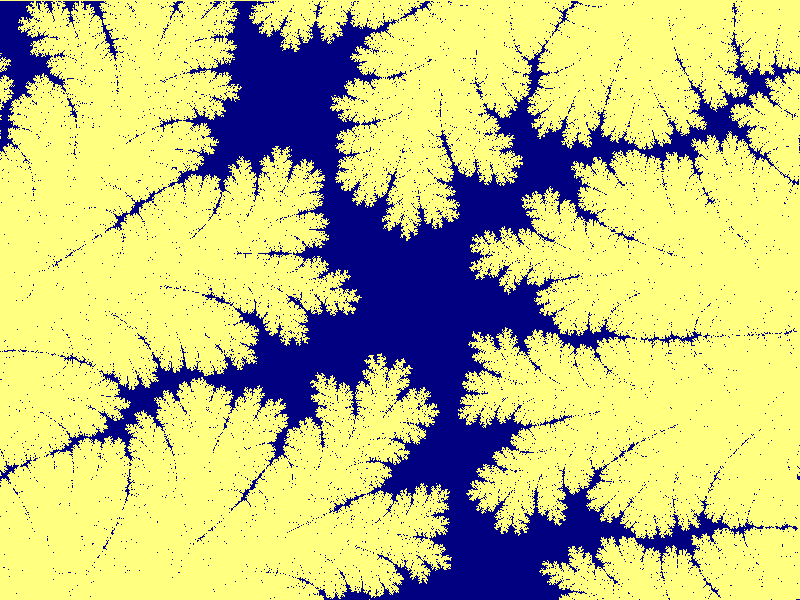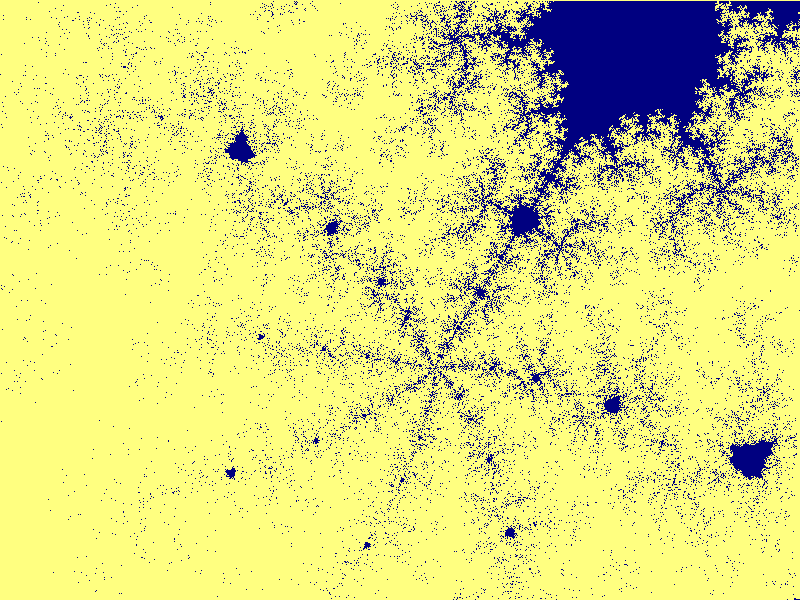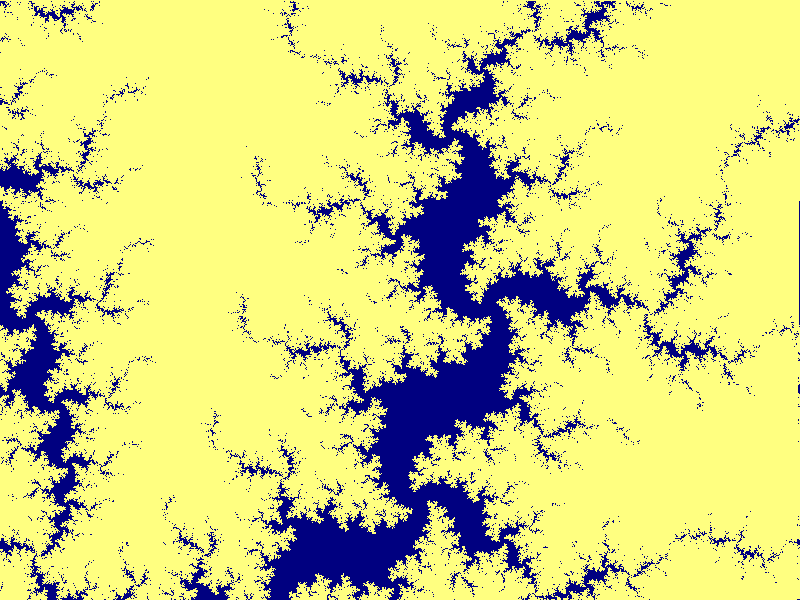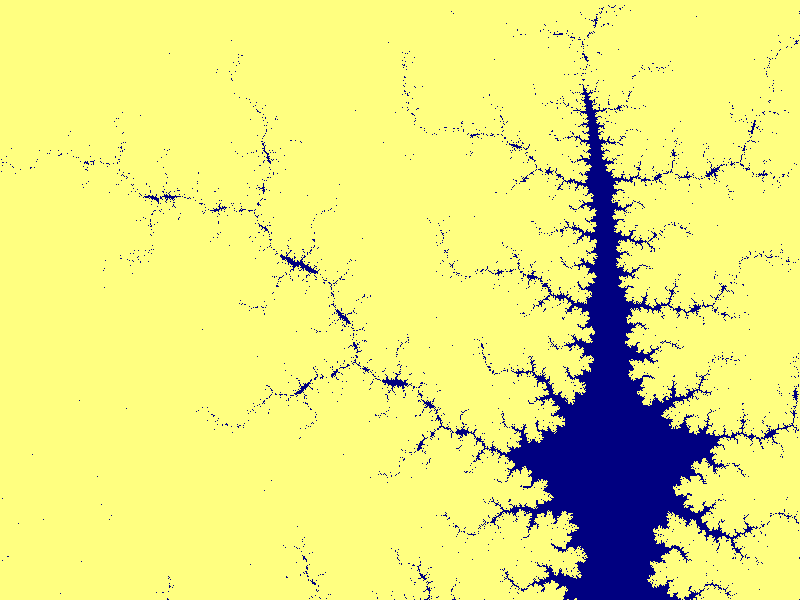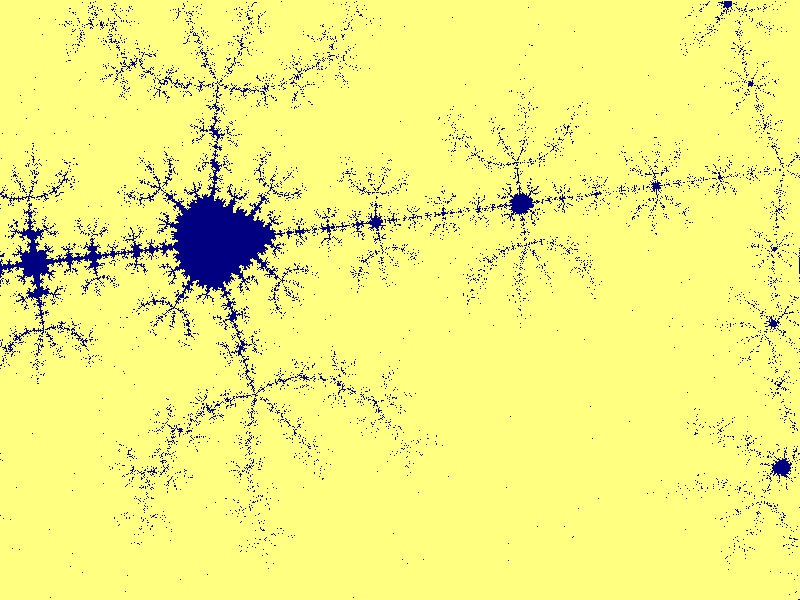Mandelbrotmängden runt punkten (-0.7472200754882813 0.06876272739257812) med bredden -9.9111328125E-7 (Biskopen)

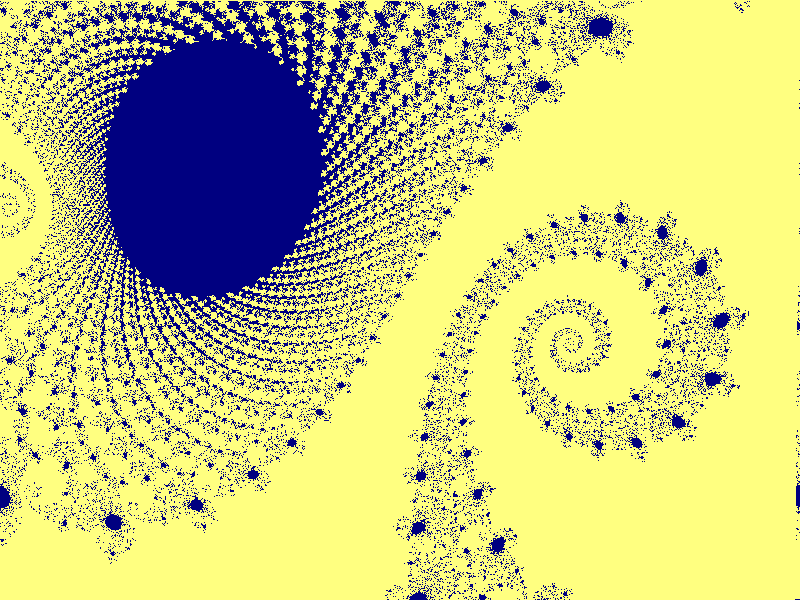Hästar:



Bläckfisk: