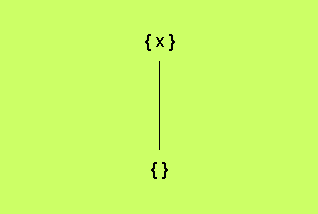Ordningsrelationer

En relation ≺ kallas en ordningsrelation, om den uppfyller

  1. a ≺ a    (reflexivitet)
  2. a ≺ b ⇒ ¬ b ≺ a om inte a=b    (asymmetri)
  3. a ≺ b och b ≺ c ⇒ a ≺ c    (transitivitet)
En ordningsalgebra är en en algebra <M, ≺ >,som består av en mängd M, som algebran 'handlar om' och en ordningsrelation, ≺ så att relationen är definierad för alla par av element ur M.

Ordningsalgebror är till för att ordna saker. En totalordning är en ordningsalgebra där för varje par a och b gäller att

a ≺ b eller b ≺ a
(eller båda om a=b). De reella talen, dvs algebran <R,≤> bildar t.ex. en totalordning. De reella talen går då att ordna upp på en linje (tallinjen)

Men det finns många exempel på motsatsen. Här är ett:

<∑M,⊆>
∑M är mängden av alla delmängder till M. ⊆ är relationen "är delmängd till". Mängden är alltså en mängd av mängder, som är tagna ur en "universalmängd" M. Relationen är den naturliga "mindre än eller lika med"-relationen för mängder.

Givet två mängder A och B, som går om lott. Det är varken sant att

A ⊆ B eller att B ⊆ A
Mängderna är alltså inte totalordnade.

Men det finns många mängder som är ⊆ än både A och B. Mängden av dem kallas L. I mängdfallet finns det en av medlemmarna i L, som är störst, i den meningen att den är ⊇ alla de andra. Den kallas skärningen mellan A och B, och skrivs A ∩ B. På samma sätt finns det en mängd U av mängder, som är ⊇ både A och B. Den som är ⊆ än alla de andra kallas för unionen av A och B, och skrivs A ∪ B.



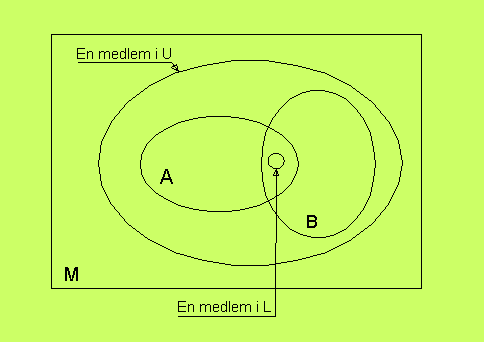
Allmännare har vi en ordningsalgebra <M,≺ >. Till varje par a och b ur M har vi

Om operationerna ∨ och ∧ existerar, så har ordningsrelationen genererat två operationer, och vi har en algebra

<M,≺, ∨, ∧>
Denna algebra kallas för ett lattice

Hasse-diagram

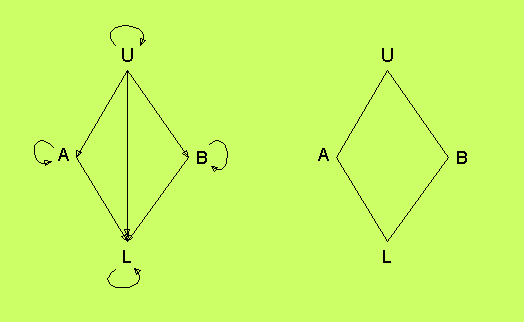
I figuren nedan till vänster har vi fyra element i M, och vi har markerat alla relationer med pilar, som ju har en riktning liksom relationerna genom asymmetrin. Till höger har vi tagit bort alla pilar, som direkt följer av transitiviteten och reflexiviteten. Dessutom har vi underförstått att alla pilar pekar snett neråt, och därmed utelämnat pilspetsarna. Ett sådant diagram kallas ett Hasse-diagram.



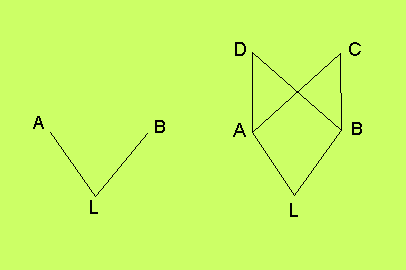
Figuren visar ett lattice. Två icke-lattice visas i följande figur. I det ena existerar inget element, som är större än både A och B. I det andra finns det två, och de är inte inbördes relaterade, så att man kan avgöra om ett av dem är större.



I en ordningsalgebra kan man ordna utmanarturneringar, där det element som är ≻:st vinner. I ett lattice finns en slutlig segrare, sedan alla element deltagit i utmaningar, och det elementet kallas Ω Det finns också en slutlig segrare i alla ≺-utmaningar, och den kallas Φ. Med hjälp av dessa kan man eventuellt hitta ett komplement c(a) till ett element a, enligt:

c(a) ∨ a = Ω

c(a) ∧ a = Φ
Om c(a) existerar för alla a, säger man att man har ett komplementärt lattice. Sedan kan operationerna ∧ och ∨ uppfylla vissa distributiva lagar, och då kallar man algebran för ett distributivt lattice. Ett komplementärt och distributivt lattice kallas för en Boolesk algebra.

Den Booleska algebra, man vanligen stöter på, den med en 1:a och en 0:a. är emellertid nog så enkel. Den har två element och följande Hassediagram:



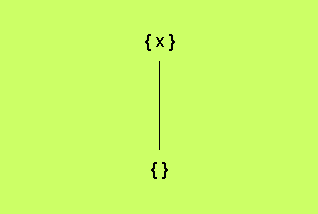
Här har vi låtit elementen vara mängden av ett element x, och mängden av inget element, dvs den tomma mängden. Relationen kan då vara ⊇. Vanligen kallar man i stället elementen 0 och 1 och definierar relationen med (förutom det som följer av reflexiviteten):

0 ≺ 1

till innehåll