Heltal

Om man vill se matematiken som läran om strukturer, så finns det en enkel struktur att börja med: mängden med sina element. När man, i Aristoteles efterföljd, gör definitioner, så definierar man ett konkret begrepp, genom att tala om ett abstraktare begrepp, och sedan avgränsa det konkreta begreppet med hjälp av sina egenskaper. Fortsätter man sedan med att försöka definiera det abstrakta begreppet, så behöver man ett ännu abstraktare begrepp. Till slut får man svårigheter med att hitta ett ännu mera abstrakt begrepp. Ordet element är ett förslag till ett ultimat abstrakt begrepp, som inte behöver definieras ytterligare. Själva ordet kanske inte alltid passar, som t.ex. när man går från talgoxe till fågel till djur till levande organism och så vidare. Men tanken med ordet element är nog ändå, att det skall fungera som det ultimata abstrakta begreppet.

Sedan samlar man ihop samlingar, eller mängder av sådana element. Det är nog den enkla tanken med mängdläran. Men att göra ett axiomsystem för läran om sådana mängder (mängdläran) bjöd på ansenliga svårigheter. Kruxet är att man måste hålla sig borta från idén om mängden av allting, som riskerar att skapa paradoxer (Russels paradox). I alla fall finns det numera ett allmänt accepterat axiomsystem för mängder efter Zermelo och Fraenkel.

Mängder har en viktig strukturell egenskap: Antalet element i en mängd. För att specificera detta antal använder vi heltal (eller egentligen "naturliga tal". Vi återkommer till detta).

Först behöver vi ett sätt att ta reda på om två olika mängder har samma antal element. Därför bildar vi par (x,y) av element, där x kommer från den ena mängden, och y från den andra. Vi ser beteckningen (..,..) som en parbildningsoperation. Om vi kan bilda sådana par, så att alla element i båda mängderna kommer med i något par, och så att inget element kommer med i två olika par, så kan vi konstatera att de båda mängderna har samma antal element.

Mängden av par är intressant i sig själv. De definierar en inverterbar funktion f. Man kallar mängden av par för graf(f); funktionens graf. Av en inverterbar funktion kan vi göra en "svart låda" i form av en kiosk. Vi går till kiosken med ett element x i den ena mängden, och får då reda på det element y i den andra mängden, som är hopparat med x. Skulle man i kiosken hitta flera y, som passar ihop med ett x, så har man gjort en felaktig parbildning.

Men sådana "felaktiga" parbildningar har sitt värde ändå, och då talar man inte om inverterbara funktioner, utan bara om funktioner. De är användbara, men inte för att jämföra antal element i två mängder.

Men med de inverterabara funktionerna, kan vi avgöra om två mängder har lika många element. Detta gemensamma antal kallas mängdernas kardinaltal card(M).

Nu behöver vi en referensmängd. Människor har i alla tider skapat en sådan med hjälp av en ramsa. På svenska har vi: "ett två tre fyra fem sex sju åtta..." eller med mera internationella beteckningar (1,2,3,4,5,6,7,8,...) Om vi stannar vid 7, så har vi

{1,2,3,4,5,6,7} = M₇

där vänsterledet är det matematiska sättet att skriva mängden av de olika krumelurena (med {}-parenteser och kommatecken). Sedan har vi:

card(M₇) = 7

Det är ju så här vi gör, när vi räknar äppen i en skål. Vi pekar på varje äpple, och säger samtidigt de olika ljuden i ramsan. Vi kan ha en kontrollant, som ser efter att vi inte pekar på samma äpple två gånger, och att vi inte missar något äpple. Sedan tar vi det sista ordet i ramsan, och säger: "Vi har sju äpplen". Vi kan också ringa till vår faster och säga detta, och fråga henne om hon har lika många äpplen, och då gör hon om samma sak, så då vet vi. Med hjälp av referensmängderna slipper vi det mödosamma arbetet att para ihop äpplena på telefon.

På ramsan måste vi ställa vissa krav. Krumeluren, som kommer efter en viss krumelur, kallar vi för krumelurens efterföljare. Varje krumelur måste ha precis en efterföljare. Därför får inte en viss krumelur finnas på flera ställen i ramsan, eftersom den då kunde ha olika efterföljare på olika ställen. Men det svåra kravet är att ramsan aldrig får ta slut. För varje krumelur i listan, måste vi veta hur man bildar efterföljaren. Det har nog alltid funnits enklare kulturer, där ramsan är ändligt lång. Det verkar som om det grönländska talsystemet slutade vid 20. Det romerska talsystemet hade ett begränsat antal symboler för att ange tal som 100, 500, 1000 osv. Men om det slutade där, med M för tusen, så kunde man kanske representera 1 miljon, genom att skriva tusen stycken M. Men vårt decimala siffersystem, som vi har nu, känner inga sådana begränsningar, så länge pappersbruken kan procucera mera papper att skriva på.

Detta krav på att det alltid skall finnas en efterföljare, är ju ändå ganska svårt. Det finns i ett axiomsystem för de hela talen efter Peano. Andra axiom i detta system handlar om addition och multiplikation, men vi skall behandla detta på ett annat sätt här.

Platon

Vi har nu givit en slags mening åt begreppet heltal, genom att se att vi kan ge dem mening, med hjälp av namn från en ramsa.

Platon skulle då säga: Vi behöver inte de namnen. Talen existerar ändå.

Mot detta skulle vi kunna ställa följande retoriska fråga: "Vad skall jag med talet 7 till, om jag inte vet vad det heter?"

Platon har kanske rätt, och han kanske också har rätt i att det finns en idévärld, där talet 7 existerar, och en sinnevärld, där vi lever. Det är kanske så, att om vi skall tillgodogöra oss idevärldens begrepp i vår sinnevärld, så behöver vi en anpassning i form av ett sätt att ge de abstrakta talen namn.

Addition

Här nu ett så kallat kommutativt diagram

Idén är att vi får samma resultat, oavsett vilken väg vi följer genom diagrammet från en punkt till en annan. En sak, som detta betyder, står längst ner till höger:

card(M₁) + card(M₂) = card(M₁ U M₂)

Det här sambandet definierar en ny operation, som vi just har hittat på: addition, +, Vi får lämna en viktig reservation här, nämligen att M₁ och M₂ inte får ha några gemensamma element. Det överstämmer med en tes om äppleskålar: "Inget äpple kan ligga i två skålar samtidigt". Så vi kan se addition som ett hjälpmedel för att räkna äpplen.

Ur denna "definition", eller snarare beskrivning av vad addition är, kan vi härleda sådant vi av vana vet om addition. En bakomliggande idé här, är att ett kommutativt diagram visar på två skilda världar, här en värld av mängder, och en värld av tal. De relaterar de två världarna, och säger här, att union motsvarar addition.

Det brukar underlätta resonemanget om de "vertikala funktionerna", här card(), är inverterbara. Det skulle betyda att givet x₁, så finns det en bestämd mängd, som är den enda mängd, som har card(M)=x₁. Så är det ju inte. Men vi klarar oss bra här i alla fall, genom att bara hitta en representant för alla dessa mängder. Som representant kan vi ju välja referensmängden, som vi har beskrivit ovan (från ramsan). Alltså, om vi vill beräkna 4 + 7, så väljer vi

repr(4) = {1,2,3,4}

Sedan hittar vi på en alternativ remsa med små primtecken (') och gör

repr(7) = {1',2',3',4',5',6',7'}

Genom denna innovation med en alternativ ramsa med '-tecken har vi undvikit att de båda mängderna har gemensamma element. Nu blir svaret, när vi går ner den högra vägen i diagrammet att

7+4 = card({1,2,3,4,1',2',3',4'.5',6',7'} = 11

vilket vi får fram genom "äppleräknarmetoden", genom jämförelse med M₁₁.

Multiplikation

Vi kan gå vidare till multiplikation. Vad är det i mängdläran som motsvarar multiplikation? Jo, det är en ganska oomtalad operation, som kallas Cartesisk produkt: ☓. Den Cartesiska produkten

M₁ ☓ M₂

är mängden av alla par (x,y), som man kan bilda genom att ta ett element x ur M₁, och ett element y ur M₂. När vi bildade funktioner valde vi ut vissa par. Men här måste vi välja alla par.

Betrakta nu följande rektangulära badrumsgolv:

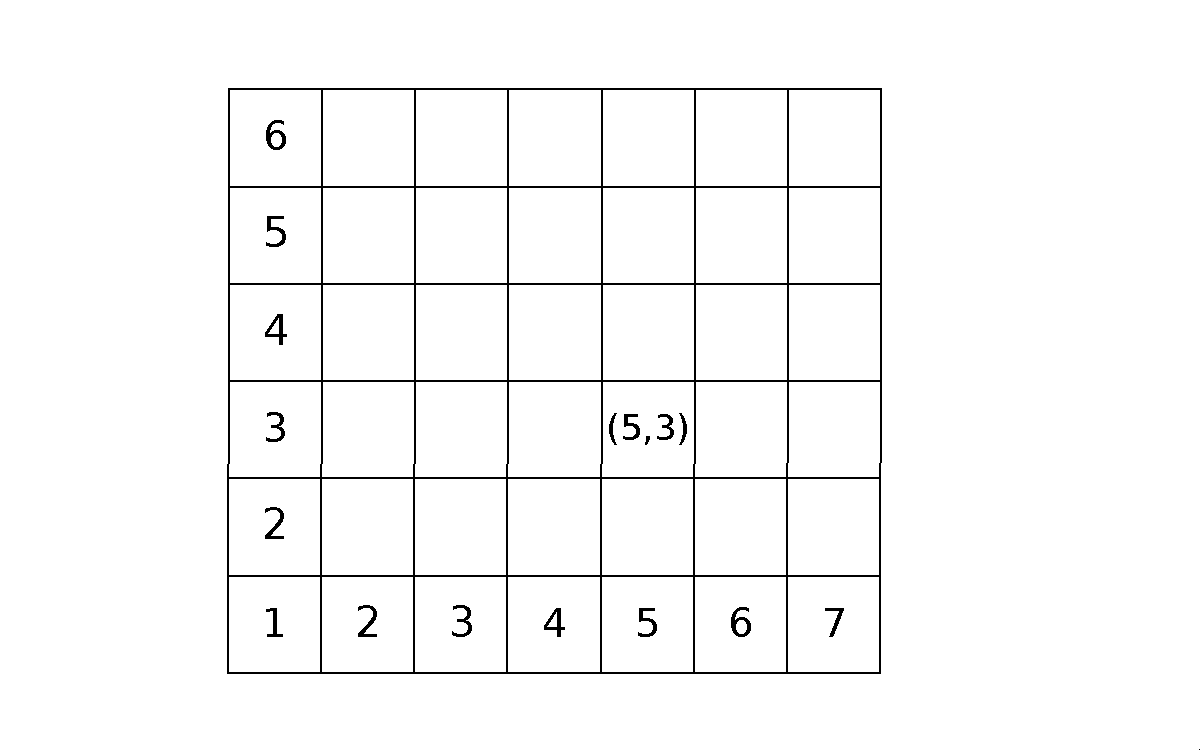
Hur många kakelplattor finns det på golvet?

Vi har satt nummer på de södra och västra kakelplattorna. Och sedan har vi skrivit in ett par (5,3) på en fritt vald kakelplatta.

Det är uppenbart att vi kan märka varje platta med ett par på detta sätt, och det är också klart att samma parbeteckning inte kan dyka upp på två olika plattor. Vi har alltså en hopparning av plattor med par. Antalet plattor är alltså det samma som antalet par:

card(plattor) = card(par) = card(M₁ ☓ M₂)

där M₁ är mängden av sydliga plattor, och M₂ är mängden av västliga plattor.

Nu skriver vi:

card(M₁) * card(M₂) = card(M₁ ☓ M₂)

som en "beskrivning" av multiplikation, *. Och då förstår vi att vi kan använda multiplikation för att räkna ut ytor (t.ex. på rektangulära badrumsgolv):

Antalet plattor = 6*7 = 42

"Upphöjt till " (xⁿ)

Vi nöjer oss här först med att hantera 2 upphöjt till n, alltså 2ⁿ.

Givet en mängd M. Med Σ_M menar vi mängden av alla delmängder till M, inklusive M själv och den tomma mängden ∅. Om vi skall göra en sådan delmängd, så måste vi först avgöra om det första elementet i M skall vara med, och det ger oss två möjligheter. Nästa element ger oss två möjlighet för var och en av de tidigare möjligheterna. Vi ser att om mängden har n element, så får vi totalt 2ⁿ sätt att göra en delmängd av M.

Alltså

card(Σ_M) = 2^card(M)

vilket tjänar som en beskrivning av vad vi kan mena med "upphöjt till". Men vi har nog också upptäckt att vi kan beskriva detta som upprepad multiplikation

Algebra

Nu kan vi gå till algebror, som vi har behandlat här . Låt oss tänka oss en grupp, och se om heltalen kan bilda en grupp. Vi skapar alltså en grupp

< N,+ > där vi har betecknat mängden av heltal med N.

Är detta en grupp?

För det första skall den vara sluten, så att om a och b är heltal, så skall a+b vara ett heltal. Detta är uppfyllt, men det kräver att vi inte låter mängden N sluta. Alltså, varje tal skall ha en efterföljare.

Sedan skall addition vara associativ, dvs

(a+b)+c = a+(b+c)

Det är uppfyllt, och går tillbaka till en motsvarande egenskap hos mängder och unionoperatorn.

Sedan skall det finnas ett additivt neutralt element, e, så att

a+e = e+a = a

Detta är uppfyllt, och e är talet 0, som vi kan definiera med

e = 0 = card(Ø)

Men nästa krav ger oss bekymmer. Det skall finnas en additiv invers a^-1 till a så att

a+a^-1 = a^-1+a=e=0

Ett sådant a^-1 kan vi inte hitta för ett positivt a, om a^-1 också skall vara positivt. Vi behöver "plötsligt" de negativa talen.. Vi har varit en liten smula förutseende här, genom att kalla mängden av våra tal för N, vilket är mängden av de hela talen, vilken också inkluderar de negativa talen. De enbart positiva heltalen kallas de naturliga talen, men dem överger vi alltså nu.

Hur skapar vi nu dessa negativa tal, eller annorlunda uttryckt namnen på dessa negativa tal? På svenska placerar vi ordet "minus" framför namnet. På "matematiska" placerar vi tecknet "-" framför symbolen för talet. Vi får -5 och -a t.ex. Nu kan vi skapa vårt a^-1:

a^-1 = -a

och vi kallar summan a +-b för a-b. På så sätt har vi uppfunnit subtraktion.

Vi har lite problem med att räkna upp alla dessa tal. Vi kan ju inte räkna upp dem, för vi vet ju inte var vi skall börja. Börjar vi på 0, så får vi inte med oss de negativa talen. Men vi tänker väl oss någonting så här:

... -5,-4,-3, -2, -1, 0, 1, 2, 3, 4, 5 ...

Vi vet ju inte hur ramsan börjar, men det är väl ungefär samma sak, som att vi inte vet hur den slutar...

Slutligen: Den hör gruppen är kommutativ, (Abelsk) för addition är kommutativ, så att a+b = b+a, vilket går tillbaka till samma egenskap hos unionsoperatorn U.

Gruppen " < N,* > ?

Finns det också en grupp med heltal och multiplikation? Nej, det gör det inte. Det neutrala elementet är nu inte 0 utan 1, för a*1 = a. Inverselementet betecknar vi åter med a^-1 och a^-1 = 1/a. Vi har uppfunnit division. Men 1/a blir inte ett heltal, om inte a antar det sällsynta värdet 1. För att hitta vår multiplikativa grupp, måste vi gå till de rationella talen. Q. Och < Q,* > är också en Abelsk grupp. Och de rationella talen tillsammans med både addition och multiplikation bildar en kropp

till innehåll