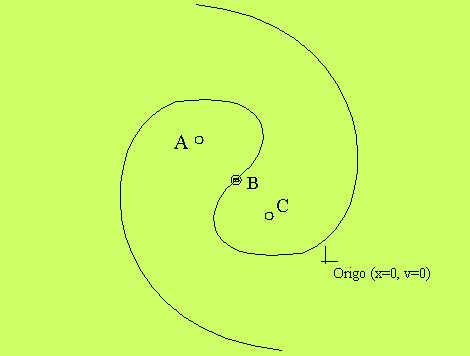Dynamiska system med insignaler

Ett system utan insignaler, som avhandlas här, kallas ett slutet system. Vi har nu dynamiska system med insignaler. Tillståndet vid en viss tidpunkt är bestämt av tillståndet vid en begynnelsetidpunkt, och av värdet av en insignalfunktion över alla tider efter begynnelsetidpunkten. All information om systemet före begynnelsetidpunkten, som har en möjlighet att påverka framtiden, finns i tillståndet i begynnelsetidpunkten. Om systemet är kausalt, så är det dessutom bara insignalen värden fram till tiden t, som kan påverka tillståndet vid t. Insignalen är i varje tidpunkt en punkt på en insignalmångfald U. Vi kan skriva:

pt = Φt-t0 (pt0, {(τ,uτ)|t0 <τ<t} )
Tekniskt är det inte lätt att formulera funktionen Φ i den här formen. Men i vektorfältsformen av ekvationen går t mot t0, och då får man
dxi/dt = X({xi},{uj})
Om vi inte vet något om u, så är determinismen borta. Vi kan inte längre förutse hur tillståndet skall utvecklas.

För att kunna göra vetenskap av detta måste vi anta något om u. Det finns några möjligheter:

Styrning

Givet systemet:

dxi/dt = X({xi},{uj})
som vi med enklare beteckningar skriver
dp/dt = X(p,u)
Om vi låter u vara en funktion av p, har vi
dp/dt = X(p,u(p)) = X'(p)
Vi har alltså på nytt ett slutet system. Vi vill nu använda funktionen u, för att ge detta slutna system (kallat det slutna systemet) önskvärda egenskaper. Vi kan ge det en attraktor, där vi önskar det, och vi kan ge den attraktorn en önskad bassäng, och en önskat snabb konvergens. I vissa fall kan vi önska oss attraktorn som ett focus, alltså med konvergens som en dämpad svängning, men oftast kanske vi vill ha en mera direkt konvergens.

Idén är att vi kan uttrycka de önskade egenskaperna i form av ett önskat vektorfält X*. Då har vi ekvationen:
X(p,u(p)) = X*(p)
Om vi vill lösa funktionen u ur denna ekvation, betraktas den som en funktionalekvation, och det är möjligt att vi kan lösa den analytiskt. Om X och X* är lineära funktioner, går det. Men vi kan också lösa u(p) som värde för ett visst p-värde, som vi råkat hamna i. Vi bestämmer alltså funktionens värden när vi behöver dem, och intresserar oss inte för funktionen u som sådan.

Robusthet

Termen robusthet handlar om att vi uppnår en acceptabel styrning, dvs ett acceptabelt slutet system, fastän det verkliga systemet avviker från funktionen X, som vi kan se som en modell av det verkliga systemet. Vi uttrycker möjligheten till variation hos X genom att införa en parameter θ, som tillhör ett k-dimensionellt vektorrum:

X = X(p,u,θ)
Nu varierar parametern θ inom ett område Θ, och för varje p och u får vi då en möjlig mängd vektorer som
X(p,u,Θ)
Vi har samtidigt en mångd Ξ* av acceptabla värden på vektorfältet. Då skall vi för ett p, som vi har hamnat i, välja u så att
X(p,u,Θ) ⊆ Ξ*(p)
Om detta inte går måste vi öka mängden Ξ* för det givna p-värdet. Systemet kan då t.ex. lokalt divergera från en önskad attraktor, men det är möjligt att systemet kan ta igen detta vid andra p-värden runt attraktorn.

Styrbarhet

För ett lineärt system finns ett begrepp, som heter det styrbara underrummet till tillståndsrummet. Om det inte är lika med tillståndsrummet självt, är det ett rum av lägre dimension. Om systemet startar i origo, kan man då inte med de givna insignalerna, u, få tillståndet att lämna det styrbara underrumet.

I det olineära fallet kan detta vara betydligt svårare att analysera. Man kan kanske inte nå en viss punkt i tillståndsrummet genom en kort resa genom tillståndsrummet, men man kan ändå nå punkten genom en lång omväg.

Om man gör en mera lokal betraktelse, så kan man nå punkter, som ligger i de riktningar som ges av X(p,u) för olika u. Låt A och B vara 2 sådana vektorer. Med tiden t kan man då nå punkter som
p0 + t·A  och

p0 + t·B
Men med ett resonemang liknande det om Lie-grupper kan man visa att man för större t kan beräkna dessa punkter som
p0 + exp(t·A) = ΦAtp0  och

p0 + exp(t·B) = ΦBtp0  och

Men man kan då också göra en sammansatt förflyttning så här:
ΦAt⃞ ΦBtp0 = ΦAt ○ ΦBt ○ ΦA-t ○ ΦB-tp0
Såsom framgår här är detta en förflyttning med en tangentvektor
[A,B] = A·B - B·A
Det betyder att även denna vektor måste vara en tangentvektor i det lokala styrbara underrummet. Ett rum, som är slutet under operationen [,] kallas en Lie-algebra. Om ett rum inte är slutet under [,] så att t.ex. [b1,b2] inte tillhör rummet, så kan man alltid lägga till denna vektor som en extra basvektor bn+1. Om man då får nya problem med t.ex. [b1,bn+1], kan man lägga till den som en ytterligare basvektor, osv. På så sätt kan man eventuellt göra en "Lie-slutning" av rummet. Men det styrbara underrummet till ett dynamiskt system är av sig själv Lie-slutet, alltså en Lie-algebra.

Insignal- utsignal-relationer

För ett verkligt system är en utsignal varje sorts signal, som man kan mäta eller varsebli. För en modell av ett system, kräver vi att sådana storheter, som modellen skall vara relevant för, skall gå att bestämma ur tillståndet, p. Vi betraktar då här en utsignal som en funktion y av tillståndet. Oftast kommer vi att tänka oss att värdet y(p) är ett reellt tal, men vi kan också tänka oss tupler av reella tal. En typisk utsignal är någon av koordinaterna för tillståndet: y(p) = xi(p).

För ett system försöker vi nu beskriva relationen mellan en insignal u och en utsignal y.

För ett lineärt tidsinivariant system kan man med hjälp av Fourier-transformteori visa att överföringsfunktionen:

G(ω) = Fy(ω)/Fu(ω)
är en invariant för systemet, dvs den är den samma för alla u. Fy och Fu betyder Fouriertransformen av funktionerna y och u. Överföringsfunktionen G är då en bra representation av insignal-utsignalrelationen.

På samma plats hittar man också en relation mellan tidsfunktionerna, som

y(t) = ∫h(t-s)·u(s)·ds
Funktion h är den funktion, som kommer ut som y om u är en kort puls. Den kallas därför för impulssvaret för systemet.

Tekniskt kan man mäta upp överföringsfunktionen genom ett enkelt experiement. Man förser systemet med ett u, som är en sinussignal med frekvensen ω.För ett lineärt tidsinvariant system blir då också y en sinussignal med samma frekvens, men med en annan fas och amplitud än u. En tidsförskjutningen med τ betraktas som en fasförskjutning med Δφ = τ·ω. För den givna frekvensen ω är G(ω) ett komplext tal med

║G(ω)║=Ampl(y)/Ampl(u)

arg G(ω) = Δφ
(arg z definiera som arctan(Im z/Re z)). Genom att variera ω kan man bestämma G(ω) för alla reella ω, och sedan kan man i princip genom så kallad analytisk fortsättning bestämma G(ω) för alla komplexa ω, för vilka funktionen är analytisk, och G är analytisk nästan överallt. Det här är inte genomförbart för instabila system, efersom de producerar en utsignal även utan insignal. För stabila system aktiverar starten av en insignal dämpade svängningar i systemet, som man måste låta klinga av innan man kan läsa av resultatet. Även en mer eller mindre abrupt ändring i frekvens kan aktivera dämpade svängningar.

Man skulle kunna bestämma impulssvaret även för ett olineärt system, men den impuls man då skall applicera, skall vara extremt kortvarig men ha extremt hög amplitud, och det tenderar att störa ut de flesta olineära system. Man kan använda andra insignaler t.ex. steg, och sedan räkna ut impulssvaret ur stegsvaret.

Tekniskt går det däremot ofta bra att göra samma experiment, som man i det lineära fallet har för att bestämma överföringsfunktionen. Man applicerar då en sinussignal med någon frekvens. Det som kommer ut är då i allmänhet inte en sinussignal, och det betyder att man särskilt måste definiera vad som menas med amplitud hos utsignalen, och vad som skall menas med fasförskjutning. I detta fall är det inte heller meningsfullt att beteckna relationen med ett komplext tal G(ω), utan det är bättre att separat tala om amplitudförhållande och fasförskjutning.

Instabila system ger samma problem som för lineära system, men det finns många fler fall. Olineära system har gränscykler, eller kan producera kaos, även helt utan insignaler, och det förtar meningen med utsignalrelationer. En del system är kaotiska just i närvaro av periodiska insignaler. Det är utan tvekan en slags insignal-utsignalrelation, men den är svår att kvantifiera. Ett system kan ha instabila gränscykler. Dem försvinner systemet då ifrån, så man kan inte se dem i längden, men de är ju egentligen en del av dynamiken. En del sådana instabila gränscykler kan finnas till följd av att det finns en periodisk insignal, och de är ju då rent av en del av insignal-utsignalrelationen, men vi kan ändå inte se dem efter ett tag.

När vi lägger på en sinussignal som insignal, så kan vi tänka oss den som genererad av ett separat dynamiskt system vars tillståndsrum är en cirkel S1. Sinussignalen bestäms ju av en fasvinkel, som är en vinkel, som representeras av en cirkel, som uttrycker den topologiska identiteten att vinkeln α är samma vinkel som α+2nπ. Vi kan då också betrakta systemet av oscillator och det drivna systemet som ett enda system med tillståndsrummet S1×M.

Såsom de två kommande exemplen visar kan mätta överföringsfunktioner vara tämligen märkvärdiga.

Exempel 1

Figuren visar följande system, beskrivet med tillståndsrummet på formen S1×M:

dx/dt = v

dv/dt = -(1/m)(kx + ζv) + A·sinφ

dφ/dt = ω



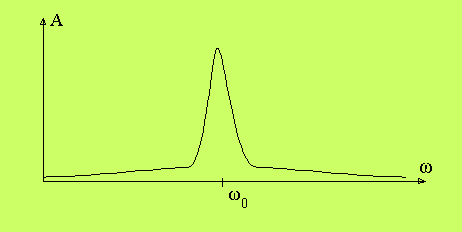
Det här är en dämpad mekanisk pendel med en resonanstopp vid en frekvens ω0 Pendeln har en fjäder med fjäderkonstanten k.

Nu lägger vi på en tredjegradsterm i fjäderkarakteristiken och får då ekvationen:

dx/dt = v

dv/dt = -(1/m)(kx + k3x3 + ζv) + A·sinφ

dφ/dt = ω

Då händer något märkligt;



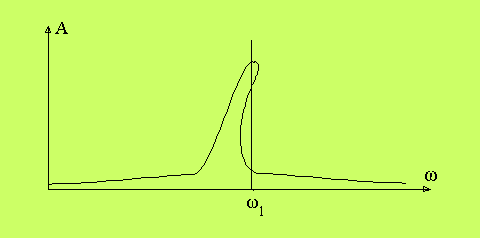
Resonanstoppen böjs! Vid den markerade frekvensen ω1 har vi tre olika amplitudförhållanden. Hur är detta möjligt? Det är möjligt, därför att det finns tre olika svängningsformer som samexisterar i tillståndsrummet. De är attraherande eller repellerande gränscykler. Vi gör en Poincarésampling, dvs vi sätter upp ett plan genom tillståndsrummet vid φ=0, och ser var tillståndet passerar genom det planet, dvs. vi ser vad x och v är då φ=0. Så här ser det typiskt ut (möjligen får någon annan vinkel än φ=0):



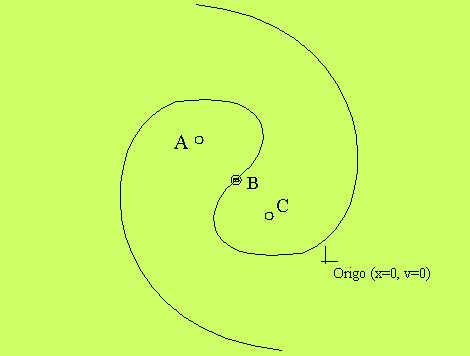
Punkterna A och C är attraktorer. C ligger närmare origo, och svarar därför för svängningen med lägre amplitud. (Detta gäller både x och v; vi har inte sagt vilken av dem som vi kallar för utsignal). De har var sin bassäng, och vilken attraktor vi hamnar i beror på i vilken bassäng vi startar. Bassängerna skils åt av den s-formade linjen, som alltså är en separatris. På den finns en attraktor, B, som är en sadelpunkt. Ur hela systemets synpunkt är den en repellator, eftersom systemet helst vill lämna separatrisen, och därmed B, för att ge sig ut i någon av bassängerna. De här tre kritiska punkterna A,B och C svarar mot de tre skärningarna mellan linjen ω = ω1 och kurvan. Punken B svarar mot undersidan av kurvan. Eftersom den är repellerande, kommer vi i längden aldrig att se någon svängning där.

När vi ökar frekvensen ω, så kommer A och B att närma sig varandra, och vid ett visst ω möts de, och utsläcker då varandra. Då kommer systemet att attraheras till den enda kvarvarande attraktorn C.

Exempel 2

Här har vi ett system med en gränscykel, som störs av en oscillator. Det totala tillståndsrummet är R2×S1. Vi gör en Poincaré-sampling där oscillatorns fas är 0. Om vi inte alls kopplar ihop de båda systemen, och om frekvensen hos gränscykeln och frekvensen hos oscillatorn är olika., så kommer gränscykeln att vara i olika fas varje gång oscillatorn passera vinkeln 0. I Poincaré-planet får vi då en cirkel, eller någon annan sluten figur. Det är den vänstra stora cirkeln i följande figur:



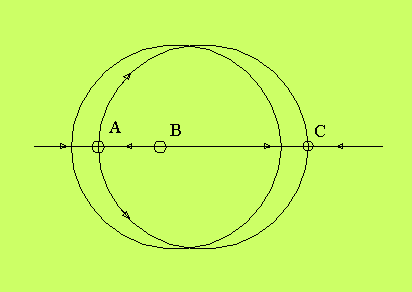
Om vi kopplar ihop de båda systemen, så kan en synkronisering ske. I Poincaré-planet får vi en konvergens mot punkten C, vilket innebär att vi har en svängning med en lite större amplitud än i det okopplade systemet. Det beror på att gränscykeln får energi från oscillatorn. Men vi har också en kritisk punkt i A på motsatt sida av origo. Den motsvarar att gränscykeln lyckas värja sig mot synkroniseringen genom att hela tiden ligga i motfas mot oscillatorn. Den är stabil i amplitud, men instabil i fas; så snart den kommer ur sin absoluta motfas, tippas hela systemet över mot synkronisering. Men det måste ändå finnas en separatris mellan A och C, och det är en instabil kritisk punkt i B.

Amplitudförhållandet A som funktion av frekvensen hos oscillatorn ser ut på följande egendomliga sätt:



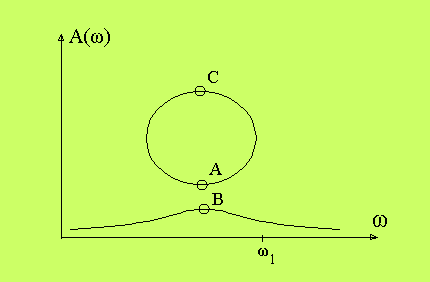
Det finns ett frekvensband, där vi får synkronisering, och det vi då ser vid en verklig mätning är den del av kurvan, där punkten C ligger. Punkterna A och B är båda instabila, så att systemet försvinner från dem vid minsta störning. Då vi kommer till frekvensen ω1 har de båda cirklarna i Poincaré planet glidit ihop, och därmed eliminerar punkterna A och C varandra. I amplituddigarammet glider de ihop, men i Poincaréplanet kan de inte det, eftersom de ligger i motfas. Nu återgår gränscykeln till sin ursprungliga frekvens, och löper asynkront med oscillatorn. Därmed har vi inte längre någon meningsfull insignal- utsignalrelation. Vad vi ser i amplituddiagrammet utanför ω1 är bara en instabil svängning på oscillatorfrekvensen, men systemet lämnar den till föremål för den asynkrona svängningen med gränscykelns frekvens.

Det var fysikern Christiaan Huygens, som upptäckte möjligheten att gränscykler kunde synkroniseras till varandra. Han var urmakare, och hade ett antal ur upphängda på en inte alltför stabil vägg. En dag upptäckte han att flera av klockorna gick exakt i takt.